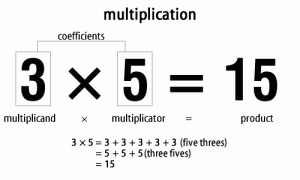
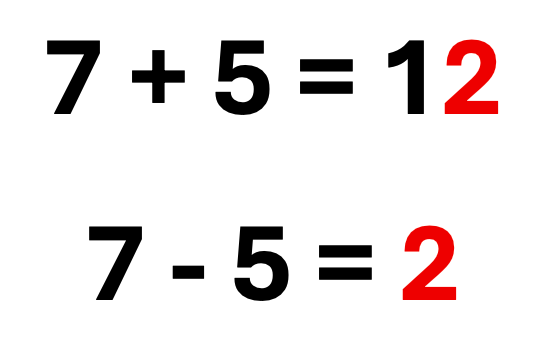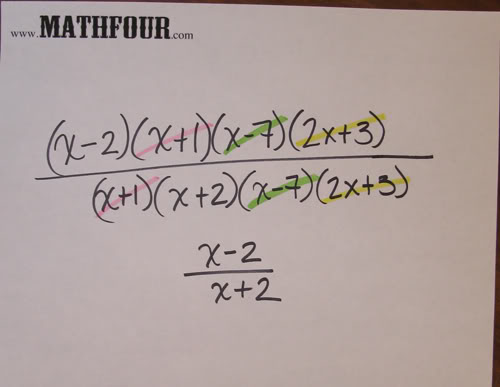I learned my math facts by “singing” them while looking at flashcards.
Having these facts ingrained with chanting or singing isn’t a bad idea. It might not “feel right” because we’re so into experiential learning these days. But if a kid can’t immediately access and use things like 8 x 7 = 56, he’s going to be slower than if he can.
And if he’s slower, he might get frustrated and start to think that he’s not good at math.
Also, knowing these cheap and dirty math facts helps with confidence. Even if a kid’s struggling with other things in math, knowing that he has this one thing (the “facts”) will help out.
I fight this battle often. Some people feel that math facts shouldn’t be memorized. But there’s so much value in it.
How about you? Which side of the fence are you on?