Did you have PEMDAS crammed down your throat? Did you hate it? Well, perhaps it’s because it’s wrong. Continue Reading →
Does PEMDAS Freak You Out?
Tag Archives: order of operations
The Absolute Value of a Number is Always…
Absolute Values of numbers might be simple, but when you start using letters with them, watch out! Continue Reading →
Another Reason to Ban PEMDAS
PEMDAS is riddled with problems. Here’s a situation where real students were directly affected by this horrid mnemonic. Continue Reading →
Math iPad App Numerosity Launches!
The latest and coolest in math games helps kids practice order of operations and other algebra plays. Continue Reading →
Exponents of Negative Numbers
Do you or your kids get a little lost when trying to deal with powers of negative numbers? Here’s a fun way to teach them. Continue Reading →
Math Rules & Their Destruction of Education
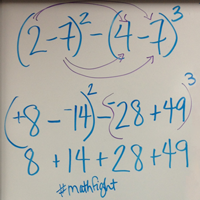
Teaching math rules to kids sounds nice, until they follow them blindly – through all their math classes! Continue Reading →
PEMDAS and a Stupid Arbitrary Rule
The order of operations is rife with rules created merely for convenience. When teaching these to kids, it’s clear how they see it as a stupid arbitrary rule. Because often it is! Continue Reading →
The Order of Operations Explained: Multiplication and Division
Last week’s article on the order of operations included a quick mention that division is the same as multiplication – but different. Now’s the time to explain that a bit. Continue Reading →
The Order of Operations Explained: Exponents, Multiplication and Addition
Next in the series explaining the order of operations is this discussion on the relation of exponents, addition and multiplication and how to remember the order of operations… the natural way! Continue Reading →
How to Teach a Weird Math Rule
Grownups are often frustrated when faced with “they made this math rule just to make me mad” – because we secretly believe that it’s true! Where did these rules come from and how are we supposed to teach them? Continue Reading →