Yesterday I shared my first experience on GeoGebra – and hinted that I had some concerns.
GeoGebra bills itself as “Free mathematics software for learning and teaching.” Indeed the intent is learning – but the market for the software is teachers.
Which means grownups are using it and then making kids use it. And we are using it as if we know what a student needs to learn math.
Yes, we occasionally do. But we have much less discovery learning these days and much more spoonfeeding.
And I worry that a powerful tool like this can easily turn into another way we can tell students:
Here, do this. It will help you learn math because it’s hands on. Make sure you follow the instructions so you can discover what you’re supposed to.
But we don’t have to let it!
The objectives are the current focus.
In the classic backwards way we teach, the “lesson plan” might go something like this:
We need to learn that the center of the circumcircle around a right triangle is the midpoint of the hypotenuse. So I’ll give them the steps to draw a circumcircle. Then I’ll teach them how to move the vertices.
I’ll construct specific questions to lead them to discover that the center of the circle will be the midpoint of the hypotenuse. They’ll certainly get it then.
And what if they don’t “discover” it on their own? It becomes another performance based failure. And then the teacher discovers it for them.
We can refocus on discovery!
I discovered math when I used GeoGebra. Math I never knew.
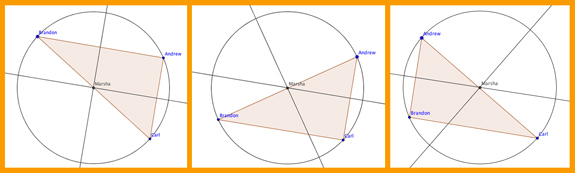
I loved watching the circles and triangles dance. From that I saw that when my point “Marsha” is on each of the sides, it appears she’s on the midpoint.
But I wasn’t answering any questions about it. I followed the instructions to draw the triangle and the circle. And then I played.
There were no leading questions. Nothing I had to “get right.” I just had fun.
Try it in class.
Suppose you gave your kids exactly what I had – instructions to draw the circumcircle and how to use the Move Tool.
And left it at that.
Would some students discover the hypotenuse/center thing?
Sure!
Would other students not?
Yepper!
And that’s okay.
I’d never heard of a circumcircle. I know “circumscribed” – but not circumcircle or circumcenter. And I’m doing pretty well mathematically.
If a child discovers something, that’s a win. If they don’t – well that’s NOT a loss! Let it go.
It’s not your job to discover it for them. No matter what the Common Core Standards or TEKS say.
See what happens…
Restructure your lesson plans. See if you can give lots of different “how-to” sheets on drawing stuff on GeoGebra. And see where their curiosity takes all of you. You just might be surprised!
 |
 |
You might also like:
- GeoGebra – Overcoming the Fear
- Curiosity Based Learning with 100 Floors iPhone App
- Creativity Destroyed
- Do Parents See the Math Monster? Or Just Think It’s There?
This post may contain affiliate links. When you use them, you support us so we can continue to provide free content!
Was a little nervous when you started, as I have a serious mathcrush on GeoGebra. I love it’s flexibility. Students can use it as a powerful tool, and teachers can design sketches that allow students to play and notice. Free so students can have at home and schools can widely install? Bonus!
It does give the impression that I’m heading to a GeoGebra bash, doesn’t it?
But I try to refrain from bashing anything and instead give options. Regardless of how a tool looks to a grownup (including me) there’s always a kid that will find it the opposite. Good or bad.
(Indeed I have a friend who would get frustrated with (and now hates) Cuisenaire Rods! And she’s a physicist!)
And there’s always something you can do to use a tool in discovery based learning. GeoGebra looks to be one of those “hero tools” – in the right hands it can save the world.
But if it falls into the wrong hands, we could be doomed.
So glad you’re one of the heros, John!
I certainly agree that teachers can use GeoGebra to better understand what they are teaching (definitely a plus). And I agree that playing with ready-to-use “interactivities” does not necessary lead to understanding or discovery (although this applies to ALL such R2U interactivities/images AND GAMES – not just those created with GeoGebra). HOWEVER, having students create their own interactivities with GeoGebra to illustrate the topic they are studying and uploading them on the internet (now extremely easy) and/or showing them on a smartboard definitely can help clarify the ideas and/or misconceptions. I have had great success with this.
Thanks for stopping by and sharing your thoughts, Linda. I love to hear about wins in the classroom!
Linda!
I just looked at the site you linked your name to (yours?). How fabulous!
I’m going to link it loud here for readers: GeoGebra Wiki at http://geogebrawiki.wikispaces.com/
Wow!
Hi Bon,
Like John, I thought for sure you were about to bash a terrific teaching and learning tool, and I am glad that you did not.
I love GeoGebra. I agree with the benefits it offers that John and Linda mentioned. I have played around with it for years.
Most of my constructs are products of my play, not constructed with teaching in mind; however, they are great for exploration and discovery of pattern and dynamical change and constancy. I initially thought about creating worksheets for the constructs but decided against it for the very reasons you presented in this post. (As an exception, my Trigonometric Laws construct does have questions which lead students to discover deeper patterns and processes, and wider connections in the Laws.)
However, GeoGebra’s potential is only as good as that of the user and guide (whether teacher or instructions). It is limited by the expertise of the user. It is also limited by the guidance provided. In a few cases, letting students play with a construct with no guidance can lead to deep discovery; however, often no guidance can lead to students 1) playing around without searching for any patterns, and 2) getting lost in an indecipherable puzzle.
The two great advantages of GeoGebra are that it allows visualization of concepts and dynamic flow through manipulation of those concepts. I believe Mason (Questions about Geometry, 1991) said that geometry is about change and constancy in movement, not about static images.
GeoGebra enables movement, bringing geometry – among other concepts – to the life it is supposed to emulate.
Great post,
Shawn
Thanks, Shawn!
You are so right. I think the reason I was initially intimidated by this thing was that I had NO guide. I opened it up, clicked a few things and got overwhelmed.
I see that the link you shared has various constructs as well as other things. Great resource!
Thanks so much for sharing!