How to Use Prime Factors to Cancel Fractions

Filed Under: Arithmetic; This post has 6 comments - join the discussion!

I previously posted about prime factors and about using them in multiplication. Now we’ve got fractions to handle.

Before we get in too deep, first let me note the main reason why we do this with arithmetic. In algebra, students will be asked to take a rational expression, factor it and reduce it like this:

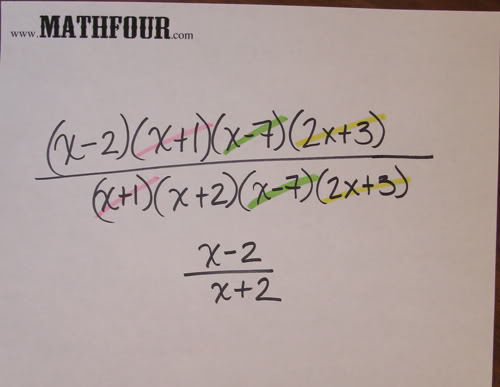
If they are familiar with how factoring works with numbers, this will be normal to them.

I also find that reducing factors in this neat and clean way helps a lot. In this video I showed the first few steps of reducing the fraction a sloppier way after I did it the “neat” way:

Here’s one that’s a little more complex:

Will be helpful to show your kids? Is there something I’m missing? Share with us in the comments.

This post may contain affiliate links. When you use them, you support us so we can continue to provide free content!

6 Responses to How to Use Prime Factors to Cancel Fractions

Douglas Hainline says:

December 22, 2011 at 4:15 pm

This post is exactly right.

Calculators are great for when you’ve got to divide (4.00376 x pi)/( 37.028^3 x sin(49.2 degrees)).

Otherwise, they get in the way of learning how numbers relate to each other, of which the addition and times tables are the start.

Is there any school in the world where teachers are still in the grip of that crazy idea from the sixties, that children should not memorize their times tables?

Reply
- Bon says:
  
  January 2, 2012 at 5:25 am
  
  Indeed, Douglass, there are people who don’t believe that memorizing times tables is worth doing.
  
  I’m presenting to a group of teachers in a few weeks on how to increase creativity by using the calculator. I should be interesting!
  
  I also wrote a few of my thoughts in this article: http://mathfour.com/arithmetic/multiplication-tricks
  
  Thanks, Douglass, for stopping by!
  
  Reply
LaToniya A. Jones (@POWEROrgMath) says:

January 10, 2012 at 1:22 pm

Bon,

I enjoy teaching with the prime factors as well. I was just speaking about the ease of using the prime factors with an instructor yesterday. Now to encourage practitioners and pre-service teachers to value “prime factorization”. That’s a task worth pursuing 🙂 It levels the playing field for students of all ages.

Reply
- Bon says:
  
  January 17, 2012 at 10:55 am
  
  Thanks for your comment, LaTaniya.
  
  It is a challenge getting teachers to embrace it if they don’t already. I hope that connecting it to working with rational functions helps them see the long term value.
  
  🙂
  
  Reply
Evan Weinberg says:

January 10, 2012 at 5:59 pm

This is great – I use a similar technique of prime factorization to teach simplifying radicals to weaker students. The circling method (rather than slashes) keeps it much more organized and legible as you simplify as compared to the slashing out.

For students lacking number sense and arithmetic fundamentals, it is a bit too abstract to say ‘find the largest number that divides the numerator and denominator’. Instead your method emphasizes that the numerator and denominator are carrying factors that are ‘extra’, and that these common factors divide out to 1. While I would encourage students to check their prime factorization with a calculator, this is an otherwise perfect opportunity for them to practice their mental math and get a good understanding of what is actually going on when we simplify fractions. Thanks for sharing!

Reply
- Bon says:
  
  January 17, 2012 at 11:30 am
  
  Thanks, Evan.
  
  Curiously, I prefer doing it this way myself. And I’m pretty okay with number sense and arithmetic fundamentals.
  
  Thanks for stopping by!
  
  Reply