Why does a word problem seem so difficult? Kids do them everyday! They can figure out if they have enough money to buy more credits on Facebook – a word problem. They can decide if they have enough time before soccer practice to watch one more TV show – another word problem.

There are two issues:

1. Too many numbers buried in too many words.
2. Teachers forcing them to use variables and fancy math-teacher ways.

Even if they can wade through the words, often it’s unclear what they’re supposed to do with all that information. Add to that a teacher forcing some variables in the mix and there’s disaster a’brewin’!

As the facilitator of their learning, you can help them to get rid of all the words that are in the way. You can show them how to experiment with drawings, approximations and arithmetic to arrive confidently at an answer. And you can do this without variables and techniques that make their eyes glaze over.

To demonstrate, I’ll use this word problem:

1. The Beebo bird lives in two places in the world. Some live in Texas and some live in Greece. Greek Beebos are about 20 inches high and weigh around seven pounds. There are about thirty-nine thousand Greek Beebos. How much do the Greek Beebos weigh altogether?

1. Read the last line first.

The question part of a word problem is usually the last sentence. If you start there, you cut to the chase. Most people like to know the point of something and then fill in the details later. The same is true with kids and word problems. “Tell me what my goal is and then tell me what I’ve got to work with.”

For our example, the question sentence is:

How much do the Greek Beebos weigh altogether?

2. Get rid of “useless” information.

The part of the word problem that isn’t the question is the “situation.” It houses all the bits that are available.

The situation often contains non-numeric information. This information could be useful, but that’s rare. So trash it from the start. Remind your students that they might have to come back to it later, just in case.

The Beebo bird lives in two places in the world. Some live in Texas and some live in Greece. Greek Beebos are about 20 inches high and weigh around seven pounds. There are about thirty-nine thousand Greek Beebos.

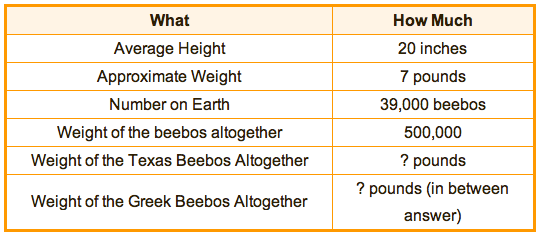
3. Put all the “useful” information in a chart.

The information in the situation that seems useful can be organized. No reason to stay buried in words if you can get the numbers out in the open. Especially if the numbers are written out and look like words!

On the left is “what the number is telling you” and on the right is “how much that value is” – including the units. Include the missing information – the answer to the question – in the chart as well.

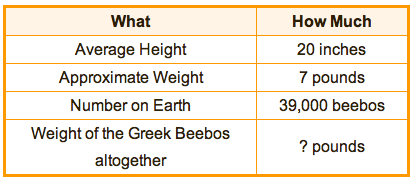
I call this the “What/How Much” chart. Fairly cheesy words, fairly straight-up concept.

4. Approximate the answer.

Have the student determine what kind of answer will make sense, or what kind of answer will not. In our beebo bird problem we want the weight of all the Greek beebos in the world as one giant blob of beebo-squish. A decimal answer like 0.4371 will not make sense. A gi-normous beebo-bird-blob is much larger!

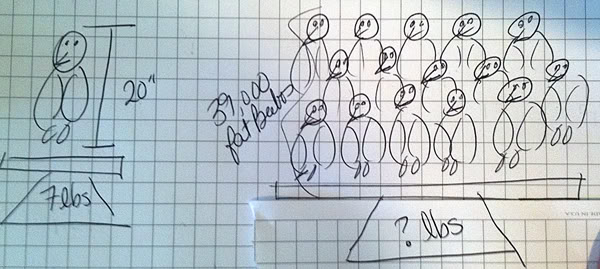
5. Draw pictures.

This is a standard tip for a word problem involving something geometric. But even if the problem has nothing in it that seems “draw-able,” encourage a drawing.

Sketching a word problem will pull the student out of the right brain and into the left brain. A little creativity for creativity’s sake will calm him down and get everyone feeling great about moving forward.

Here’s my drawing of our beebo bird problem:

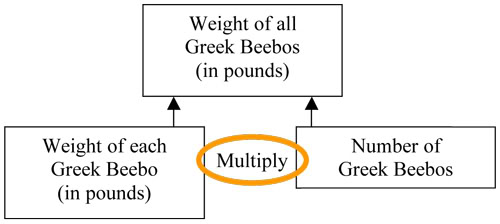
6. Make a flow chart.

A flow chart will help the student understand which pieces will be used to get the answer. In our example, there isn’t a whole lot of work. But we see that because we’re pretty experienced in doing these things.

A kid could use the flowchart to see that, indeed, there isn’t anything else to be done.

Start at the top with the final answer. Have them work their way down using the pieces that are needed to get to the answer. If they know it, or can quickly figure it out, it is also helpful to include the operation. This piece isn’t necessary though – in number 7, below, they can dig around and figure the operation out.

Put the arrows pointing upward to show that the work will be done in that order.

To give this demo a little more oomph, Let’s modify problem #1 just a bit to give us problem #2:

2. The Beebo bird lives in two places in the world. Some live in Texas and some live in Greece. Greek Beebos are about 20 inches high and weigh around seven pounds. There are about thirty-nine thousand Greek Beebos. The total weight of all the beebos in the world is 500,000 pounds. How much do the Texas Beebos weigh altogether?

The flowchart for problem #2 starts with the final answer on the top (the weight in pounds of all Texas Beebos) and works its way down using the pieces necessary. The data below a box is what it takes to get the answer listed inside the box.

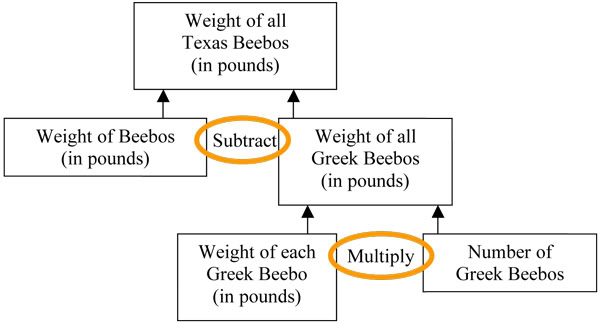
Notice that the What/How Much chart you would have done for this word problem will need to be flexible. It isn’t until you make this flowchart that you realize there is another piece of necessary information to calculate before you can calculate the final answer. It’s the “in between answer” for the weight of all Greek Beebo birds. You can stick it at the bottom of the chart with a note:

7. Use trial & error to pick the answer that makes sense.

I’ve already put the operations on the flowcharts above, but your student might not be clear on them at that stage. Here’s the time to let them experiment.

They can look for keywords to determine the operation, but that can feel like another forced “pixie dust math” trick. Let them go through their own discovery process and they’ll figure out the keywords for themselves.

Demonstrate that it’s okay to get the wrong answer a few times before getting the right answer. Typically, you’ve only got four operations: addition, subtraction, multiplication and division. They shouldn’t have to use exponents, roots or logarithms at this point.

Let them use all four operations on the numbers. With the approximation they did in number 5, they will be able to eliminate at least one of the answers. Allowing them to get their hands dirty with all of them will give them confidence. It’s like making their own multiple-choice problems!

Conclusion

Although these tips are written in an order, many are interchangeable. Especially numbers 4, 5 and 6. Encourage your kids to use these but don’t force it as another algorithm. Use these as guidance toward discovery.