This is the 5th in the series The Order of Operations Explained. For the other articles in this series, click here to visit the introduction.

Last week’s article on the order of operations included a quick mention that division is the same as multiplication – but different. Now’s the time to explain that a bit.
The only thing mathematicians like to do more than create, is destroy. That’s how we get imaginary numbers, dividing by zero and raising things to infinity.
Once we create with multiplication, we want to know what happens when we destroy with the opposite of multiplication.
Enter Division, stage right.
Multiplication is created from the need to quickly add a bunch of numbers that are all the same. They each must be equal to make this work:
6 + 6 + 6 + 6 + 6 is shortcutted to 5 X 6.
Division is the breaking up into pieces that are all equal.
Technically we can break 30 up into these 5 pieces: 4, 8, 7, 6 and 5. But “division” requires (or implies) that we are dividing equally. So 30 would have to be broken up into 5 equal pieces of 6 each.
Of course this is in a purely mathematical world. When you get into a toddler world, things will be different.
How division is the same as multiplication.
We represents multiplication with little x‘s or dots or stars. Like this:
3 X 5 or 3 • 5 or 3 * 5
We represent division with this cute little symbol:
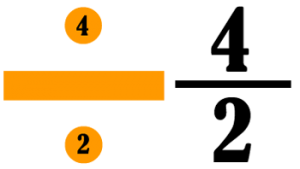
But we can write it in many more ways. Notice the cute symbol looks like a fraction with dots on the top and bottom. That’s not a coincidence. A fraction means division.
Remember the poem:
When dividing fractions
Don’t bat an eye
Just flip the last
And multiply!

Well, you can change this to:
When dividing numbers
Don’t bat an eye
Just flip the last
And multiply!
And “flipping” the last just means taking the “assumed 1” that’s underneath it and putting it on the top.
Now go forth and divide…
So when you’re teaching the MD in PEMDAS, the order of operations, remember that D is the same as M. And if things get a little confusing, demand some parenthesis before doing the problem.
Share your thoughts in the comments!