This is the 2nd in the series The Order of Operations Explained.
For the other articles in this series, click here to visit the introduction.

I mentioned in the introductory article for this series that “the order of operations isn’t best practice for expressions involving variables.”

When you involve a variable, you can’t just “do” the arithmetic. Like in the case of 2(3x + 4)=11. You can’t add 3x and 4 to get a result before moving on. You have to use the distributive property.

And even the distributive property won’t work sometimes – as in the case of absolute values shown below.

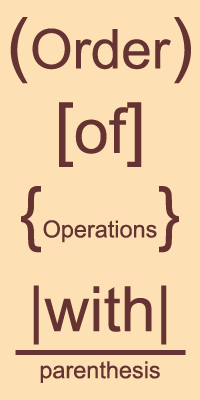
Parenthesis mean isolation.

When we say “parenthesis” in the Order of Operations (OoO for short), we mean anything that’s grouped together and isolated. This could mean with actual parenthesis. This could mean [square brackets] or {curly brackets}.

Although grownups seem to know that square and curly brackets are the equivalent of parenthesis, children don’t. This has to be said out loud.

“Parenthesis” in the OoO can also mean |absolute value bars|. This one’s not so clear.

When you try to solve the equation 4|2x+3|=20, you have to start with dividing by 4 to isolate the absolute value chunk. There’s not a “rule” for distributing the 4.

(Although, it would be worth it, and fun, to see if your children can come up with some rules for distributing within absolute value bars. This would be some real mathematics at work for them – experimenting and discovering.)

Tops and bottoms of fractions are implied parenthesis.

It’s also the case that the numerator (top) and denominator (bottom) of a fraction are isolated places. These fall under the OoO as parenthesis.

Check out this older video I did. It shows how this works with fractions:

Parenthesis are for deviation from the other rules.

I had forgotten about this, but David Chandler of Math without Borders in the previous article:

The rule is to do higher level operations first. Use parentheses whenever your intention is to deviate from this rule.

If you can focus on this instead of a mnemonic device, you can get students to internalize what’s going on with the OoO. It’s important, however, to make sure they remember about other bracket shapes as well as isolation.

Let us know your tips and thoughts on the P in PEMDAS!

Related articles

• How Calculators Inhibit Learning the Distributive Property in Algebra
• 6 Confusing Terms in Mathematics
• How to Step Things Up in Math Teaching

This post may contain affiliate links. When you use them, you support us so we can continue to provide free content!