The two most commonly used operations in math are addition and multiplication.
And although we intermingle addition with multiplication (along with division and subtraction), these two can only mix using the distributive property.
How the distributive property works
Multiplication, in a crude sense, is a shortcut of addition. Like 3 x 8 is the number 8 added to itself three times. Or 8 + 8 + 8.
Look at 3 x (6 + 2). This is the number (6 + 2) added to itself three times. (Refrain from adding those two together, no matter how tempting. Leave them separate as 6 + 2.)
So we have (6 + 2) + (6 + 2) + (6 + 2).
And we know that when it comes to only adding, we don’t need any parenthesis. Which gives us
6 + 2 + 6 + 2 + 6 + 2
Also, addition is commutative. So we can scramble these numbers around.
6 + 6 + 6 + 2 + 2 + 2
And if we want, we can squish them together in parenthesis (seems lame, but stay with me…)
(6 + 6 + 6) + (2 + 2 + 2)
And, hey! We know that 6 + 6 + 6 means 3 x 6 (and the same with 2’s) so we have:
(3 x 6) + (3 x 2)
Remember what we started with. Put it together with what we ended with. And we’ve just demonstrated (the long way) that
3 x (6 + 2) = (3 x 6) + (3 x 2)
or, more visually…
3 x (6 + 2) = (3 x6) + (3 x2)
This is the Distributive Property of Multiplication Over Addition. (That’s the fancy name for the distributive property.)
It works with something else, too…
Since exponents are a shortcut of multiplication, we can play the same game.
Consider (6 x 2)3
This is (6 x 2) x (6 x 2) x (6 x 2)
And we can get rid of parenthesis and scramble:
6 x 6 x 6 x 2 x 2 x 2
And re-group:
63 x 23
Showing that:
(6 x 2)3 = 63 x 23
This, by the way, is the Distributive Property of Exponentiation Over Multiplication!
Yes — this IS useful.
Seems ridiculous, right?
But when learning algebra, students often get lost when faced with 3(y + 2). “What do I do now?” they think, going into panic mode.
If they know that y is just a number with lipstick on (as a disguise), they can think about the above example.
Remembering what it means is the key to knowing what to do with the algebra stuff!
What do you think? Share your thoughts in the comments or on twitter/x.
I’ve known enough women, both young and “old,” who have joined the horribly unfortunate club of breast cancer survivors. And I sometimes wonder how it is that I still forget every month to do my breast exam.
Especially when you look at the math!
5 seconds of breast exam per breast/month x 2 breasts = 10 seconds/month
10 seconds/month x 12 months = 120 seconds/year or 2 minutes/year on your breast exam
TWO MINUTES PER YEAR!
2 minutes/year x 90 years = 180 minutes or 3 hours
Can you use 3 hours of your life to do your breast exam?
And what does 3 hours of time gain you?
If you feel that tiny pebble when you do your short breast exam you can get to the doc quick. Which means nabbing that bundle of evil cells before they go any further.
Taking 10 seconds to do your breast exam means having a lumpectomy instead of a mastecomy – and possibly lymphadenectomy along with it.
Spending merely two minutes each year on your breast exams means surgeons can get that nice margin around the lump. It means preventing those damaged, multiplying cells from cruising your system and getting into other parts of you.
It means living longer. For you. For your partner and friends.
For your kids.
Cancer is the only place where muliplication sucks for everyone.
Multiplication is normally the bomb. It rocks. It’s cool.
Even if someone’s not good at it, multiplication give you the ability to triple your income. It lets you be ten times smarter than you were three years ago.
With multiplication you can love someone twice as much tomorrow.
But the multiplication that cancer cells do, destroy all of this.
So do your part.
Donate to the cause or attend a special event that supports breast cancer awareness.
And do your breast exam every month. Let your kids keep their mom.
The math shows that it only takes a little while to gain you a long while.
Do it!
I’m heading to the Houston Aeros Breast Cancer Awareness Hockey Game today. They were sweet enough to send me a bundle of tickets and I’m honored to help them raise money for the Young Survival Coalition. Tomorrow I’ll write about the math in hockey!
I’ve been stumbling over baby Jesuses for a few weeks now. I realized that with three working nativity sets in the house it was time to do a little math with Jesus.
All of them.
You can count the bits and pieces.
Animals, people, buildings – count them for each nativity set and count them up total.
How many total Jesuses do you have?
How many angels?
How many “visitors” does Jesus have?
How many sheep? Cows? Donkeys? Camels?
How many total animals?
You can compare the numbers.
My three nativity sets have varying numbers of characters and structures. It’s curious how some sets include more animals that visitors – and some sets don’t have any animals.
Which of your nativity sets have more animals? Which has more people?
Which has more buildings (or non-people/non-animal things)?
Are there more visitors than animals or more animals than visitors?
Arrange the sets in order of least to greatest – people, animals, etc. Are they always in the same order?
Is one set bigger or heavier than the others?
Do some arithmetic.
Take the opportunity to show how counting and arithmetic are kinda the same thing.
If you add up the number of sheep you have with the number of donkeys, how many is that? Is it the same if you group them together and just count them?
What if all the shepherds left? Talk about how you can count them, or you subtract the number of shepherds from the total number of visitors.
How many nativity sets do you have? Talk about how 3 times that number is the number of wise men you have.
Do fractions – but only if you must.
I know many people avoid fractions. I wish I could have avoided it with Math with Jesus. Daughter gave us the opportunity to talk about fractions by breaking the angel (or the “butterfly” as she calls it). Good thing we have Gorilla Tape.
Here’s a FREE Activity Packet to read and share with your children to get them thinking about how numbers got started.
Somewhere in the past we recognized that we have these “digits” on the ends of our hands. Using these, we created numbers, adding, subtraction, multiplication, division and even fractions!
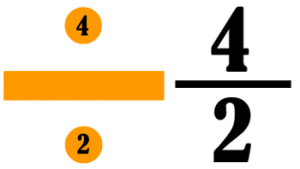
This is a guest article by Caroline Mukisa who publishes Maths Insider.
Does your middle- or high-schooler know their times tables? If the answer is a resounding “Yes” then, great, have a great day, and read the other great tips here at MathFour.
I also have some great tips and advice on how to guide your child to maths success on my Maths Insider site.
If not, then it’s time to help your teen develop their own times tables boot camp.
Why are times tables important at all?
Well it’s used loads in algebra, and those geometry questions usually need a fair bit of multiplication or division. It’s also great for those grown-up things that they’re going to be doing in the years to come, working out payment plans, home remodelling, calculating sale prices and just plain making sure that they’re not ripped off in life.
Of course we’ve got computers and calculators, but who wants to be fiddling about to open a smartphone app, just to work out the price of a pair of jeans. And if they press the wrong buttons, how will they know the answer is wrong?
Yep, they’re important!
Why are times tables a problem for older learners?
It’s like spending years trying to pass a driving test. Or still not being able to conjugate Spanish verbs after studying them for ages. Or trying to lose those last few pounds of weight. It sucks, and it gets to the point where it’s easier to develop a work-around: catch the train everywhere, just get by with a few Spanish phrases, or buy bigger clothes.
Of course, your teen can “get by” and may even do rather well at maths without knowing their times tables. But before you give up, try some of the following strategies to help your teen make their own times tables bootcamp to fix those essential times tables facts in their heads. It’s never too late!
Times tables boot camp strategies
1) Figure out what they know, and what they don’t know. Are they fine with their 2’s, 3’s and 4’s and 5’s but shaky after that? Then focus on quickly reviewing the easy tables before some concentrated repetition of the harder tables.
2) Use incremental steps. Make sure the 5’s are solid before moving on to the 6’s and the 6’s are fast before moving onto the 7’s.
3) Give your teen a fixed target. It’s completely possible to learn the times tables from 2-9 in a month with just 5-10 minutes of daily study.
4) Let them choose their own activities. Worksheets won’t be a popular option – iphone apps, You Tube videos, online games are all things that teens are more likely to tolerate.
5) Be encouraging – don’t say, “That’s easy, you should know it” instead say, “I can see you’re working hard on this, keep it up.”
Use these strategies to help your child plan their own successful times tables boot camp, so they won’t have to just “get by” in maths any longer.
Caroline Mukisa is a homeschooling mom of 4, who publishes at Maths Insider.
Last week’s article on the order of operations included a quick mention that division is the same as multiplication – but different. Now’s the time to explain that a bit.
The only thing mathematicians like to do more than create, is destroy. That’s how we get imaginary numbers, dividing by zero and raising things to infinity.
Once we create with multiplication, we want to know what happens when we destroy with the opposite of multiplication.
Enter Division, stage right.
Multiplication is created from the need to quickly add a bunch of numbers that are all the same. They each must be equal to make this work:
6 + 6 + 6 + 6 + 6 is shortcutted to 5 X 6.
Division is the breaking up into pieces that are all equal.
Technically we can break 30 up into these 5 pieces: 4, 8, 7, 6 and 5. But “division” requires (or implies) that we are dividing equally. So 30 would have to be broken up into 5 equal pieces of 6 each.
Of course this is in a purely mathematical world. When you get into a toddler world, things will be different.
How division is the same as multiplication.
We represents multiplication with little x‘s or dots or stars. Like this:
3 X 5 or 3 • 5 or 3 * 5
We represent division with this cute little symbol:
But we can write it in many more ways. Notice the cute symbol looks like a fraction with dots on the top and bottom. That’s not a coincidence. A fraction means division.
is the same as .
Remember the poem:
When dividing fractions Don’t bat an eye Just flip the last And multiply!
Well, you can change this to:
When dividing numbers Don’t bat an eye Just flip the last And multiply!
And “flipping” the last just means taking the “assumed 1” that’s underneath it and putting it on the top.
Now go forth and divide…
So when you’re teaching the MD in PEMDAS, the order of operations, remember that D is the same as M. And if things get a little confusing, demand some parenthesis before doing the problem.
The Order of Operations can be boiled down into three “real” operations.
Parenthesis are merely a way to group things – they aren’t a real operation. So they doesn’t count as a real operation.
Since division is really just multiplication turned upside down, we don’t need to include it separately, either. Likewise, subtraction is addition on its ear. So we throw him out, too.
Now we have only three: exponents, multiplication and addition.
You see that 3 x 3 x 3 x 3 is 34. The exponent is the shortcut for multiplication.
Multiplication is the shortcut for addition.
Likewise, when we get overwhelmed with adding up the same numbers over and over, like in the video, 4 + 4 + 4 + 4 + 4, we can use multiplication to shortcut it: 5 x 4.
Follow the shortcut evolution.
The shortcut evolution is like this
Addition came first.
Then we created multiplication to make addition easier.
Then we created exponents to make multiplication easier.
So when you do arithmetic, we should do the “recent” shortcuts first (exponents) and then the “older” shortcuts (multiplication) and then the “regular” arithmetic (addition). Remember that subtraction is addition and division is multiplication.
And keep in mind that we need to watch the grouping or anything isolated with parenthesis, absolute value bars or in a fraction. The grouping/isolation tools always trump the other operation rules.
What if your answer isn’t the same as the back of the book?
Some textbooks actually have multiplication done before division. This means that the problem 9 ÷ 3 x 2 will show a different answer (3/2) in that textbook’s solution pages than what you would get following the OoO I’m describing here (6). These texts are rare, but I’ve seen them. So keep your eyes peeled.
The Order of Operations is a set of rules that we’ve agreed on. Which means that as long as a textbook clearly defines their order that they will follow, they can do things like this.
If you get confused as to which to do first, demand parenthesis. (Yes, you can do that.) Or put parenthesis into your child’s textbook to help them out.
The problem sets should be there to enforce, not confuse.
What do you think? Does this help or hinder the way you’ve always viewed the Order of Operations? Share your thoughts in the comments.
Thanks to Molly for this question she left in the comments, “Why is a negative times a positive, a negative?”
“Sign – One Way” by Andrew Schmidt
It’s common to hear a child say, “They created this rule just to make me mad.”
And on the heels of that usually comes a frustrated teacher’s comment of, “No, this has a purpose.”
When then faced with, “Okay… so what’s the purpose?” a teacher or parent might become more frustrated. It’s not always clear the purpose of things like the rules for multiplying differently signed numbers.
It may also be that the grown-up secretly believes that this was all created just to make us mad. After all, when the last time you had to multiply a negative number times a positive number in the real world?
I, personally, can’t ever remember a time when that case has come up outside of a math class or tutoring session.
Then why create the rules at all?
The truth is that many math rules are created because we need a rule to continue working – something to agree on among peers working on the same project. We need everyone on the same page.
This agreement somehow gets filtered down to the kiddos as “this is the absolute way it is – do it because we said.”
So it very much looks like we created rules to make them mad.
Good deduction, kids.
How do they pick the rules?
“Street Chess” by Petr Kratochvil
Some math rules are created arbitrarily just so we have something (anything) to agree to. Like the rules of a game. The order of operations is one such situation.
There is no natural reason why we’ve chosen to do multiplication and division before we do addition and subtraction. No more so than the people in the US have decided to drive on one side of the road whereas the people in England, Australia and the Bahamas drive on the other.
We’ve agreed to it.
It keeps us from crashing.
Sometimes, we agree to a rule because it is “less bad” than any of the other possible rules we can think of. The result of any number raised to the zero power is one of these. 30 feels like it should result in either zero or 3. But if you mess with all the other rules (in particular the one about subtracting exponents here ) you’ll see that 30 really needs to be 1. If it were anything else, it would mess up the rule of .
Why is a negative times a positive equal to a negative? Is it because it messes other things up or is it an arbitrary rule? Instead of explaining the reasoning to a child, allow them discover it.
Have a “King for a Day” day where the students get to rewrite a particular math rule. Allow them to sit as a class or family and decide on the rules for multiplying signs numbers.
Give them plenty of time to experiment and see if the new rule messes anything up. (If your administrators or math curriculum specialists fret about you allowing students this time, note to them that the students are behaving like real mathematicians. They are inventing a concept or rule and testing it out to see what happens.)
If the students discover that the new rule has dire consequences when applied to the rest of our number system, they then see the reason for the rule. And they’ve learned through experience and solidified the rule in their minds!
If the students discover that there are no consequences of the new rule, they can then determine that the rule was created arbitrarily and agreed upon for convenience. It is a rule for rules’ sake.
You can discuss with them how things would be different if they kept the new rule and everyone else in the world followed the old rule. Again experience and discussion will solidify the “real” rule.
So the next time you’re faced with “why?” regarding a math rule, give it a shot. Let the children be the rulers of their own math world!
Will it work? Did it work? Share your thoughts in the comments!
I mentioned in the introductory article for this series that “the order of operations isn’t best practice for expressions involving variables.”
When you involve a variable, you can’t just “do” the arithmetic. Like in the case of 2(3x + 4)=11. You can’t add 3x and 4 to get a result before moving on. You have to use the distributive property.
And even the distributive property won’t work sometimes – as in the case of absolute values shown below.
Parenthesis mean isolation.
When we say “parenthesis” in the Order of Operations (OoO for short), we mean anything that’s grouped together and isolated. This could mean with actual parenthesis. This could mean [square brackets] or {curly brackets}.
Although grownups seem to know that square and curly brackets are the equivalent of parenthesis, children don’t. This has to be said out loud.
“Parenthesis” in the OoO can also mean |absolute value bars|. This one’s not so clear.
When you try to solve the equation 4|2x+3|=20, you have to start with dividing by 4 to isolate the absolute value chunk. There’s not a “rule” for distributing the 4.
(Although, it would be worth it, and fun, to see if your children can come up with some rules for distributing within absolute value bars. This would be some real mathematics at work for them – experimenting and discovering.)
Tops and bottoms of fractions are implied parenthesis.
It’s also the case that the numerator (top) and denominator (bottom) of a fraction are isolated places. These fall under the OoO as parenthesis.
Check out this older video I did. It shows how this works with fractions:
Parenthesis are for deviation from the other rules.
David Chandler of Math without Borders commented this in the previous article of this series:
The rule is to do higher level operations first. Use parentheses whenever your intention is to deviate from this rule.
If you can focus on this instead of a mnemonic device, you can get students to internalize what’s going on with the OoO. It’s important, however, to make sure they remember about other bracket shapes as well as isolation.
Let us know your tips and thoughts on the P in PEMDAS!
