Tag: right triangle

  • Cuisenaire Rods Go Pythagorean!

    Cuisenaire Rods Go Pythagorean!

    I’ve been playing with the lovely Cuisenaire Rods for a few weeks now. I made the (fortunate) mistake of creating this flower in a past article about coordinate pairs.

    The mistake was that I would eventually have to come up with the coordinates for this thing. Fortunate because it gives the MathFourTicians out there something else to teach with the rods!

    The center of the flower is the place to start.

    Since all the “petals” are attached to the center, that’s probably the best place to begin.

    I converted to something I could see.

    Since everything is tiny (1 cm), I went to a bigger setup. And some of the coordinates were easy to pick out. So I put those in the big grid, too:

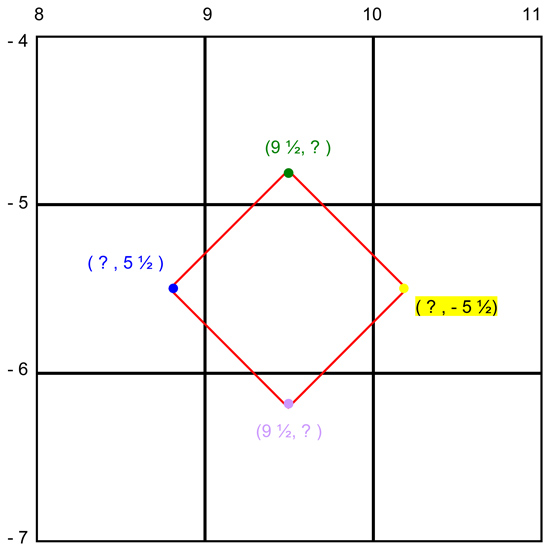
    And then I started to do some work…

    Next I considered what I was really dealing with: a square. And each side was 1 cm.

    According to those crazy Pythagoreans, the diagonal measures 2\sqrt2:

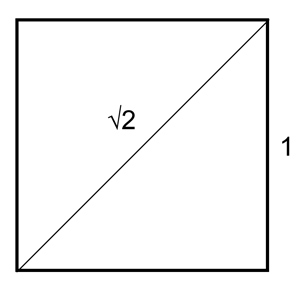
    So half the diagonal is 22\frac{\sqrt{2}}{2}:

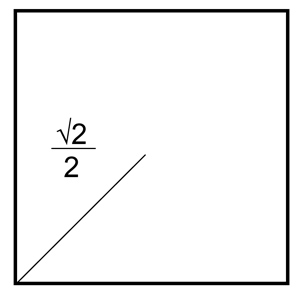
    I went back to the big grid.

    When I put this information on the big grid, it looks like this:

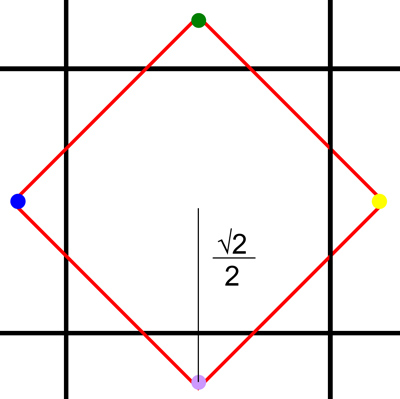
    Doing some arithmetic and geometry, I get:

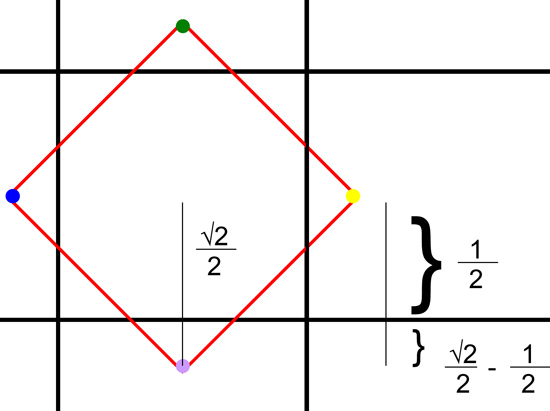
    Using my very cool TI-30 calculator, I get that 22−12≃0.2\frac{\sqrt{2}}{2}-\frac{1}{2}\simeq0.2.

    I can accurately name the points!

    Knowing that each corner pokes out roughly 0.2, I can calculate the coordinates:

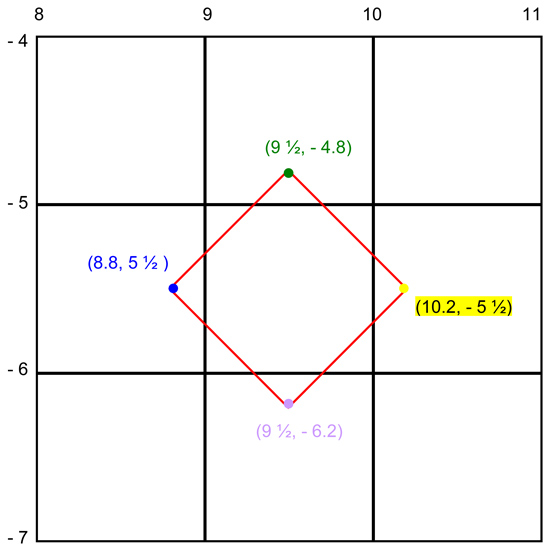
    From this I can create the ordered quadruples as described here for the petals of the flower. But at this point I’m pretty much needing a break. So I’ll leave that for next time.

    Whatcha think? Fun? Share your thoughts in the comments and on Twitter:

    Related articles
  • How to Teach Right Triangles when Crossing the Street

    How to Teach Right Triangles when Crossing the Street

    This morning Daughter and I went to the gym.

    When we crossed the street, I exposed her to undo risk by crossing at an angle.

    So on our way out, I explained to her that we were walking a little further to get to the car this time. And we would minimize the risk of getting hit by a car by taking the longer route.

    (Of course she’s not yet two, so she really didn’t care. But it was important for me to say.)

    Crossing at an angle is shorter than going straight across.

    People most often cross the street at an angle. Intuitively we know it’s shorter. Look at the tiny person in this picture. He needs to get to the front door of the store.

    It’s five yards to go at the angle, while if the little guy walked straight across then up, it would be seven yards.

    Suppose walking one yard takes 5 seconds. It will take the little guy 15 seconds to cross the street straight across. (And with a toddler, it does take 5 seconds to walk a yard.)

    Then he has to walk the four yards along the side to the door. Which means his total time is

    3 yards across at 5 seconds per yard = 15 seconds

    4 yards up at 5 seconds per yard = 20 seconds

    Total walking time = 35 seconds

    If he went at an angle, it’s 5 yards total (by the Pythagorean Theorem).

    5 yards diagonally at 5 seconds per yard = 25 seconds

    Total walking time = 25 seconds!

    Crossing at an angle puts you at risk for longer.

    For the pedestrian in a hurry (and wearing the shirt that reads “Safety Third”) the angled route is the way to go. But for a parent with toddler in tow, minimizing risk is a better option.

    If the little guy were to cross at the angle, he’d be in front of the oncoming cars for 25 seconds. If he were to take the route that is longer overall, he’d be in front of oncoming traffic for only 15 seconds.

    The car doesn’t care what angle you’re walking, it can squish you pretty easily either way.

    Not to mention he keeps the driver happy.

    Getting out of the driving area faster means keeping the driver happy. That might not be your goal, but adding some cosmic happy juice into the world of drivers never hurts.

    Plus, if someone were to “hypotenuse you” by taking the angled route when you were driving, wouldn’t you get a little annoyed?

    Next time you practice safety, practice math!

    So be safe. And tell your children why.

    It’s all about the math!

    Share your thoughts in the comments.

    Related articles

  • Learning Right Triangles with Discovery Toys

    Learning Right Triangles with Discovery Toys

    I hosted a Discovery Toys party the other day and ended up explaining how to use many of the toys for teaching math.

    Alas, here I am now doing videos of the same. I can’t get over these toys. They are designed proportionally (the cups and weighing ones) and always with the thought “How can this be fun at the same time it’s teaching something.”

    Of course, all toys teach. But the designers of these toys put the extra oomph into the thinking process so that when a kid asks “why?” there’s an easy way for the parent to answer.

    Oh – and they are guaranteed for life!

    So from here out, I’ll be doing occasional videos on how to use them.

    The first is about right triangles on the Giant Pegboard. Notice in the video that when I say “congruent triangles” I really mean “similar triangles“.

    See what you think:

    Have you played with triangles and pegboards? What other ways can you use them to teach and learn?

    Disclaimer: I tried to become an affiliate of these toys to help pay for this blog. Alas, they don’t have an affiliate program. The only way was to become an official consultant. These toys are so cool and helpful, that I have done it.