Tag: fractions

Why It’s Okay to Add Denominators when Adding Fractions
I did some videos for avoiding finding a common denominator and why this trick works. Ever since then I’ve pondered what it would look like if you added without a common denominator.

A mom on the Living Math forum was asking for advice on how to teach adding numerators and not adding denominators in fractions. So this topic is again in the front of my mind.

First note, that you can add both numerators and denominators – this is called piecewise addition – but then you are getting into a whole new world of stuff. Actually, you’ll be experimenting with some goodies from Abstract Algebra (my field of study). We’ll talk about how and why this is good in a few paragraphs.

What is adding fractions, anyway?

For us in the “real world,” adding fractions is adding values that can’t be counted with fingers. It’s adding bits of things together – maybe whole things with bits, even.

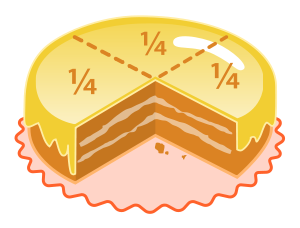
We have agreed to use things that look like

$\frac{\text{some number on top}}{\text{some number on bottom that isn’t zero}}$

to represent fractional pieces of a whole.

When we add $\frac{1}{2} + \frac{1}{4} = \frac{3}{4}$ we have said that our total is

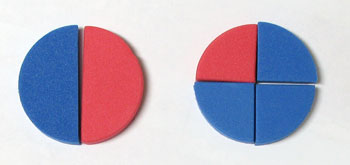
$\frac{\text{3 pieces of a whole pizza}}{\text{when the pizza is cut into 4 equal pieces}}$

Total: 3/4 of a “pizza” is blue.

Quantity over value is important to young children.

I remember taking money from Little Brother when we were kids. You might think I was stealing, but it was more of conning the innocent. He would have 3 dollar-bills. I would have 20 pennies.

He would quite willingly trade his 3 monies for my 20 monies. For him, this was a matter of quantity. I knew the value, though. (Bad girl – sorry, LB I owe you. xo)

This measuring of quantity, rather than value was important in LB’s development. Instead of someone teaching him how to measure value, he learned it through experience.

This is why we should allow kids to add the denominators.

Let’s use the example above and add the numerators and the denominators to see what that means.

Adding $\frac{1}{4} + \frac{1}{2} = \frac{2}{6}$ means that our total is

$\frac{\text{2 pieces that we have}}{\text{6 pieces that were possible to have}}$

Notice here you can’t “reduce” the fraction – because this isn’t the value as we know it.

If you teach adding fractions using manipulatives or toys and allow adding denominators, soon your children will see that your (on the top in the picture below) is very different than having their , on the bottom.

We have six total pieces.

This will inspire them to work toward equality – and invent fractional addition (correctly) on their own!

Tell us how it goes in the comments!

Related articles
June 22, 2011
6 Confusing Terms in Mathematics
Thanks to David Ginsburg for inspiring this post.

Do you struggle explaining to your students what “simplify” means? Do you wonder why they won’t reduce fractions to their lowest terms?

Here’s how to explain and teach some of the top confusing terms in mathematics – without throwing you or your students into a tizzy!

Where

Really! “Where.”

As in “Where do the lines intersect?” or “Where is the highest point of the graph?”

“Where” in math almost always means “at what x-value?” Every now and then “where” can mean “at what point?” In the first case, “Where do the lines intersect?” can be just as easily satisfied by a point (x, y) as the x-value only.

When you get into calculus, the word “where” is used everywhere (pardon the pun). “Where is the slope of the tangent line equal to zero?” and “Where are there discontinuities?” among others.

Keep your eyes peeled in the textbooks for this tricky term.

Reduce

Typically this means to reduce to lowest terms. Which isn’t really helpful, since you still need the definition of “terms.”

Numerators and denominators (tops and bottoms of fractions) that have one or more common factors are not officially “reduced.” Once they have no common factors at all (except 1), they are said to be reduced or reduced to lowest terms.

A reduced fraction helps in many ways. You can “feel” the value more easily: 2/5 is a lot easier to picture than 14/35. Also, when you add fractions, starting out with all the numbers in their reduced form will often help to find common denominators.

Zeros, Real Zeros and Roots

Zeros, real zeros and roots all mean the same thing. It is where a graph passes through the x-axis. We can write “where are the zeros” meaning at what x-value (“where” from above) does the graph pass through the x-axis? We also will write “what are the zeros” and mean the same thing.

To find the zeros or roots, we set a function (or any equation solved for y that involves x) equal to zero. Then we solve for x. This will give the result that we want – the x-values where the graph will go through the x-axis.

We call them zeros because they are where y = 0. We call them real zeros because there can be complex or imaginary zeros that don’t exist on the graph.

Finding the zeros or roots of a function help when graphing it. If you know all the places it goes through the x-axis, you can then determine where it’s above or below the x-axis. Then you can roughly sketch the graph.

Simplify

Of all the terms in mathematics, this one is the most slippery. This meaning of this term is always in context to the book or situation. What it means is “manipulate the expression.” The end result may or may not be “simpler” than the starting expression.

Better textbooks use phrases that are clearer, like “multiply the polynomials” and “combine like terms.”

If “simplify” is the instruction to a problem set in a textbook, consult the examples to see what type of manipulation to do.

In later courses, students have to recognize when a situation requires a different form of the expression. Practicing various forms of manipulation (or “simplifying”) gives them tools to manipulate the expression to satisfy their needs.

Do you run into other terms in mathematics that are hard to explain to students? Hard to understand yourself? Share them in the comments!

Related articles
June 6, 2011
What’s the Domain, Why You Need It and How You Get It
As you teach domain and range, do you get the question, “Why are we doing this?”

No doubt the question, “When am I ever going to use this?” comes up too, right?

I’ve asked myself that question my whole teaching and tutoring life. And now’s the time for an answer.

A function is really a question.

As I wrote in a previous post, a function is a question with only one answer to a valid question.

When I write:

y = 3x + 2 where x = 4

I mean: “What is three times a number (that number is four), plus two?”

The domain is all the possible questions:
- What is three times a number (that number is five,) plus two?
- What is three times a number (that number is six,) plus two?
- What is three times a number (that number is seven,) plus two?
- What is three times a number (that number is eight,) plus two?
- <how long will I have to do this – Egad!>
Not only do the questions go on forever, but they also have all the fractions and decimals in between. And all the negative versions of those numbers (and zero).

So, what’s the point, you might ask. Looks like the questions go on forever and you can just pick any number.

The domain might not include all the numbers.

The two sticky points for the definition of “function” are bolded:

A function is a question with only one answer to a valid question.

The “valid question” part is where the domain comes in.

The numbers that make “valid” – meaning we actually can get some answer – are the numbers that aren’t negative.

Many functions have “all real numbers” as a domain. There are no limits on the things you can put in, other than numbers that aren’t imaginary or alligators.

For the most part, there are only two places where you have to be careful of limited domains. Those are
- Numbers that cause a zero to turn up in the denominator
- Numbers that cause negatives to turn up in square roots.
Here are two videos tackling each:

What do you think? Is this easier to teach when you consider “analyzing” the function rather than “solving” it? Share your thoughts and tips in the comments!
May 20, 2011
Adding Fractions: Why Avoiding Common Denominators Works

I wrote this post showing that adding fractions can be done using the algebraic definition of addition of rationals:

$\frac{a}{b}+\frac{c}{d} = \frac{ad+bc}{bd}$

MathHeadInc (via twitter) has requested a video showing why this works.

I aim to please.

Here is the video showing why adding fractions using a common denominator is the same as the definition of addition of rationals:

What do you think? Will this help convince your kids that “the trick” is okay to use? Share your experiences in the comments.

April 5, 2011
How to Never Find a Common Denominator Again

Do you keep struggling to teach common denominators? Do your kids just not “get it”?

Well, it’s time to quit.

Yep! You can teach (and do) fractions without ever finding a common denominator.

The key is in the definition of addition for rational numbers. If you have two numbers and the sum of them is .

Granted there is the technical issue of reducing, but using a little prime factorization will get you there without an issue. (And you don’t really HAVE to reduce, which I will discuss in a later post.)

Here is an example:

Here’s one with an obviously easy common denominator that works just fine with this method. In it I explain a little about why you would want to do it this way:

You might argue that finding a common denominator is an important learning experience. And you’re right. In the same way that learning about death through the loss of a pet is an important learning experience. But if you can avoid all that pain, why wouldn’t you?

If you teach this method first, kids will get annoyed with having to do so much reducing and discover the common denominator method for themselves. And that’s really what learning math is all about.

What do you think? Can you teach fractions this way? Share your thoughts and experiences in the comments.

Thanks to @padgets for our conversation about teaching fraction on #mathchat a few weeks ago. You inspired this post!

March 23, 2011
How to Use Prime Factors to Cancel Fractions

I previously posted about prime factors and about using them in multiplication. Now we’ve got fractions to handle.

Before we get in too deep, first let me note the main reason why we do this with arithmetic. In algebra, students will be asked to take a rational expression, factor it and reduce it like this:

If they are familiar with how factoring works with numbers, this will be normal to them.

I also find that reducing factors in this neat and clean way helps a lot. In this video I showed the first few steps of reducing the fraction a sloppier way after I did it the “neat” way:

Here’s one that’s a little more complex:

Will be helpful to show your kids? Is there something I’m missing? Share with us in the comments.

March 2, 2011
How and When You Can Manipulate Square Roots

Square Roots (aka radicals) are part of the multiplication world. They have the same properties, but because they look weird – living in little “houses” – it is hard to grasp what they can do.

This is how the “houses” (the radicals) can “move”:

After that, you can work with multiple radicals:

It is important to note that this little trick works because it’s all multiplication, division and roots. If you have addition or subtraction in there, you’ve got yourself a challenge. Watch this to see how to deal with addition in the mix:

Thanks to jrobbo at MyMathForum.com for the inspiration for this post.

February 9, 2011
What the Heck Is the Zero Product Rule?

The fancy answer is, “For all numbers a and b, ab = 0 implies a = 0 or b = 0.”

The less fancy, and still strange answer is: If two things multiply to get zero, one or both of them better be zero. Like this:

Too much pixie dust, for my taste. What doesn’t work, for sure, is this:

So why does it work with zero and not three?!? To answer this, we need a little background on fractions and zero. And pizza – pizza’s always a good thing to add to math:

Using the fact in the video above, the “foorp” in this video shows why it’s true:

Special thanks to GFC at MyMathForum.com for inspiring this post.

February 4, 2011
2 Ways to Multiply Mixed Numbers

Multiplying fractions provides an interesting challenge. Put some mixed number into the situation and you could be facing a real bear.

Here’s one way to work the problem $2 \frac{3}{4} \times 8 \frac{1}{7}$ by converting it to mixed numbers:

Or you can use the handing dandy distributive property (or as some might recognize it – FOIL):

Here’s one more for fun:

Thanks to NapNinja4 on MyMathForum for this question.

February 1, 2011
How to Convert Mixed Numbers to “Improper” Fractions

This isn’t something you do everyday. Therefore it would be helpful to know how to remember it long term.

The mixed number $2 \frac{3}{4}$ really means $2 + \frac{3}{4}$ .

Notice the PLUS sign? That’s the big key to doing this.

This video shows the long expanded way that most people won’t show you. You wouldn’t really convert this way, but it helps to see it in the long form. This way you know what your teacher is showing you isn’t some pixie dust magic:

Now that you can do that, you can probably go the other way too:

And how about checking your work? Nevermind the devil box (aka the calculator), the more you check your own work by hand, the more your confidence in your own math abilities will be. Try doing this:

What do you think? Will this help you remember? Do you have another way to remember? Share it in the comments.

January 31, 2011