Category: Algebra

Equality and Comparison: Some Ways to Think of Equality
Equality is a big part of learning math. The equals sign means more than just “here’s the answer.” This is the second in a series on equality and comparison. For the rest of the series, click here.

It’s part of our DNA to assess the world around us. As soon as a baby sees Mommy different from Daddy (or smells the difference), she starts comparing. When she figures out that there are more than one of something, things get even more interesting.

Give each of two toddlers a ball. Then stand back and watch. If they aren’t exactly the same ball, one of them will want to switch, and the other will say no. It won’t matter which ball is truly superior, only that one child will soon perceive inequity in ball ownership.

If they are given the same color and size ball, you can watch their little brains calculate this and work to discern some difference.

And it doesn’t stop at kids. Women do it all the time. Is my bottom as big as hers? Do we wear the same size shoes (and will she let me borrow hers if we do)? Is my dress more expensive than her dress?

Comparison in math corresponds to comparison in the world.

Some things are really exactly the same.

Your two crystal champagne flutes you bought for your wedding are likely the same. Not only is one interchangeable with the other, but you couldn’t tell the difference if you were to switch them.

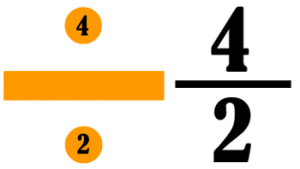
This can get a little sticky for math. There is only one number 3.

But when I write 3 = 3, there are really 2 threes running around. (Math friends: I realize two champagne flutes are not the same as two number 3s. But making analogies in the real world is tough if you don’t take a little poetic license.)

Sometimes things have the same value.

Have you ever traded a dollar bill for 4 quarters? Those aren’t exactly the same (you would be able to tell the difference if you replace one with the other) but they have the same value.

If you return a blouse to a department store that your weird uncle Zeno gave you, and get a blouse that fits your style much better, these will have the same value. Monetarily speaking, of course.

If you ship your G7 back to Canon when it’s under warranty, and they return a G10, the value to them was equivalent (while the value to you has increased).

Some things have the same size and shape.

When you replace the transmission in your car, you’re doing so with an equivalent copy that’s better than what you already have. If you replace the engine in your 1969 Mustang with a souped-up model, you’re playing the same game.

In both these situations, the replacement version, although superior in functionality, is the same in size and shape.

Sometimes things are interchangeable.

Like in the example above, with the cars, as long as one thing works equally as well as the other, you can compare them and call them “equal.”

If you reach for a pen from the pen jar on your desk, any pen will work as well as any other.

The two pens may not be exactly the same, have the same value or even be the same size and shape. But you can interchange one for the other when writing a check.

And sometimes equality is merely perceived.

Like the toddlers with the balls from above. Different people will put different value judgments on items. So there is the case that equality is in the eye of the holder. Or wanter.

What does equality mean to you?

As we progress through this series, we’ll see how equality and the equals sign in mathematics relate to equality in the real world. And thinking about how equality in the real world works is the first step.

So what do you think of when you think about two things being equal? Share your thoughts in the comments.

Related articles
September 26, 2011
Algebra with Stamps
I mailed out the bulk of the thank you notes for Daughter’s 2nd birthday party gifts. And wouldn’t you know it, it involved algebra!

I have so many stamps from the last 20 years, in every denomination you can imagine. I’m trying to use them up because I only save full sheets of stamps. (I’m a bit of a stamp collecting snob.)

Rule #1: No more than the required postage on any letter.

It has to be exact.

As of this writing, postage in the US is $.44 per letter.

I have $.33 stamps, $.37 stamps, $.41 stamps, etc. And I’ve purchased $.01, $.02, $.03, and on up to supplement and make my postage exact.

Rule #2: No more than 2 stamps of the same kind on a letter.

I like variety.

With these requirements, here are some of the combinations that I’ve come up with:

So how is this algebra?

Here is an algebra equation from the stamps in the picture:

10x + 17y = 44

The equation means x number of 10 cent stamps plus y number of 17 cent stamps will give me the exact total of 44 cents! So x=1 and y=2.

And here’s another:

10x + 24y = 44

The equation means x number of 10 cent stamps plus y number of 24 cent stamps will give me the exact total of 44 cents! So x=2 and y=1.

It would make it a better set of algebra problems if I allowed more than two types of stamps. But I’m sticking with my variety rule. 😀

How about it – will it make writing thank you notes with your kids more fun? More challenging? More annoying? Share your thoughts in the comments!

Related articles
September 20, 2011
Playing with Algebra Concepts
I’ve been itching to get into some basic abstract algebra goodies. With the help of the Cuisenaire Rods, Simply Fun Sumology number tiles and the Discovery Toys Busy Bugs, I’m able to do that.

Start with wrap around addition.

This type of math is officially called “modular arithmetic.” We are only going to use the numbers 0, 1 and 2.

It begins as regular addition. And since we are only using those three numbers, all our answers have to be either 0, 1 or 2. So when we add 1+2, we wrap around.

If we were to count in our system, we’d say: “0, 1, 2, 0, 1, 2, 0, 1, 2, 0, 1, …”

The addition table looks like this:

(Notice you could do this with numbers from 1- 12 and it would be clock addition!)

Now things get buggy.

Switch out all the number tiles with some pretty color Cuisenaire Rods. They don’t have to be the “right” rods. We’re only looking at the colors. Here’s the progression I did:

The end result is a very abstract chart!

You can “bug” two things together.

Like this:

(I know – a spider isn’t a bug. But run with me on this, okay?)

Notice that each of these are directly from the “spider table” above.

You can read this as, “Purple spider green equals green,” just like you would say, “Zero plus one equals one.”

And then turn your child loose!

First make a chart, or download this one.

You can, but don’t have to, start out with numbers. The rules are this:
- You can only use three colors.
- All three colors must go across the top.
- All three colors must go down the left.
- Fill in the 9 spaces however you want, as long as it’s only those three colors.
I did this one with the blue beetle as the “addition” piece:

So what can you do with a goofy “blue beetle table”?

Let your child play, for one. And experiment.

You can also talk about commutativity and associativity, identities, inverses… but I’ll leave that for another article!

What do you think? Does your child want to play like this? What else can you do? Share your thoughts in the comments.

Related articles
August 30, 2011
Equality and Comparison: Introduction
I’m fascinated by how the simple is really the most complex. Just proving that the two assumptions

3 + 0 = 3

and

3 + x = 3

will force x to also be 0 is a serious and important proof. And harder to do than you think.

When we get even more basic and talk about equality and comparison, things get impossibly complex.

And that’s the fun in the challenge inspired by 2nd grade math teacher, Suzanne Weider. She wrote:

Another idea I have been looking into has to do with the equal sign: teaching it as a symbol that means “the same as” as opposed to the sign that comes before the answer.

Equality and comparison are everywhere.

Some people are obsessed with fairness. Almost all people have some sense of fairness. This means that things need to be roughly equal, if not the same, for all situations in life.

We go into every situation assessing what’s the same and what’s different. Which means a judgment call on equality.

The beauty of this is that you can tap into how our natural comparison connects with the comparison tools of mathematics. These are tools like the greater than, less than and equals signs. This can set your children up for some hard-core success in algebra, geometry, calculus, and Radon-Schure-Greenlee Mathematics. (I made that last one up, but I mean crazy everything math.)

Equality and comparison are so complex that a single article won’t hold all there is to write about it. So this is the first in a series.

The series will run roughly like this:
1. Introduction to comparison (That’s this one.)
2. Some Ways to Think of Equality
3. Why People Aren’t Equal
4. Other comparison tools
5. The reflexive property
6. The symmetric property
7. Transitivity and substitution
8. Playing with the equals sign
9. Ranges and estimation
10. Inequalities and ordering
I’m excited and overwhelmed. Ready for the ride, MathFourTicians? Hold on – it’s gonna get weird!

Related articles
August 27, 2011
Order of Operations Explained: Addition, Subtraction and Conclusions
This is the 6th and last in the series The Order of Operations Explained. For the other articles in this series, click here to visit the introduction.

I started this series over a month ago. In that time, I’ve gotten pretty deep in thinking, learning and reading about the order of operations. I’ve seen a variety of ways people view, use and teach it.

Before I go too far into some conclusions, though, let’s look at addition and subtraction.

Subtraction is the same as addition.

Yup. You might remember that from the fourth article.

Consider the problem . Moving from left to right, and doing both subtraction and addition as we come to them, we get 4. If we found a book, or person, that meant the full-on PEMDAS and wanted addition done strictly before subtraction, then we would end up with 0. The latter is because we would do the addition of 3 and 2 before we did the subtraction.

Which is right?

It depends on what you really mean. If you don’t know if you should go left to right or strictly addition before subtraction, either look in the textbook you’re using or demand parenthesis.

The text will clearly outline the order of operations it’s following. Be careful, too because there isn’t always agreement among textbooks. I have seen some texts that instruct the learner to do multiplication first and then go back and do all the division signs. While others (and this is more common, today) have us do multiplication and division from left to right, simultaneously.

If you compare contemporary texts to each other, you’re likely to find them all the same. But grab a math text from the 80s at Half Priced Books. I’ll bet you’ll find at least 50% of the time they put division strictly after multiplication. (I’ll verify this the next time I’m there.)

The order of operations needs context.

I have $5 in my bank account. Then I bought a coffee for $3 and a bagel for $2. I might accidentally write down . I still mean, “I need to add up the stuff I spent and subtract it from my balance.” I wrote it in error, though. What’s “mathematically” correct is .

But you knew what I meant.

This was a typo that was helped along by using the context.

Until there’s a reason to do arithmetic, the order in which we do things is arbitrary. If we all agreed to do addition first, then multiplication, we would calculate and come up with 35 (instead of 23).

As long as we all come up with the same thing, we’re fine.

“We” have agreed to do multiplication things before we do addition things. So “we” would come up with 23 in the example.

Coach G noted it correctly: the order of operations is a convention. In other words, we’ve decided on it. We invented it.

How can you use this to teach your children?

The coolest thing is that you can let them play. Get dirty. Break it.

Remember opposite day? Have that. Let your little one make new rules. Let them see what happens if you all decide one day to do multiplication before addition. If your child is older and doing some algebra, this will mean reversing the order in which you UNDO the operations too!

This is a real brain stretcher. But it’s just math. You’re not building a bridge or balancing your checkbook. Let them break it. Let them see what happens if you make your own rules.

And then they’ll really learn!

Let me know how it goes – share your stories in the comments.

Related articles
July 17, 2011
The Order of Operations Explained: Multiplication and Division
This is the 5th in the series The Order of Operations Explained. For the other articles in this series, click here to visit the introduction.

Last week’s article on the order of operations included a quick mention that division is the same as multiplication – but different. Now’s the time to explain that a bit.

The only thing mathematicians like to do more than create, is destroy. That’s how we get imaginary numbers, dividing by zero and raising things to infinity.

Once we create with multiplication, we want to know what happens when we destroy with the opposite of multiplication.

Enter Division, stage right.

Multiplication is created from the need to quickly add a bunch of numbers that are all the same. They each must be equal to make this work:

6 + 6 + 6 + 6 + 6 is shortcutted to 5 X 6.

Division is the breaking up into pieces that are all equal.

Technically we can break 30 up into these 5 pieces: 4, 8, 7, 6 and 5. But “division” requires (or implies) that we are dividing equally. So 30 would have to be broken up into 5 equal pieces of 6 each.

Of course this is in a purely mathematical world. When you get into a toddler world, things will be different.

How division is the same as multiplication.

We represents multiplication with little x‘s or dots or stars. Like this:

3 X 5 or 3 • 5 or 3 * 5

We represent division with this cute little symbol: $\div$

But we can write it in many more ways. Notice the cute symbol $\div$ looks like a fraction with dots on the top and bottom. That’s not a coincidence. A fraction means division.

$7 \div 3$ is the same as $7\times\frac{1}{3}$ .

Remember the poem:

When dividing fractions
Don’t bat an eye
Just flip the last
And multiply!

Well, you can change this to:

When dividing numbers
Don’t bat an eye
Just flip the last
And multiply!

And “flipping” the last just means taking the “assumed 1” that’s underneath it and putting it on the top.

Now go forth and divide…

So when you’re teaching the MD in PEMDAS, the order of operations, remember that D is the same as M. And if things get a little confusing, demand some parenthesis before doing the problem.

Share your thoughts in the comments!

Related articles
July 10, 2011
The Order of Operations Explained: Exponents, Multiplication and Addition
This is the 4th in the series The Order of Operations Explained. For the other articles in this series, click here to visit the introduction.

The Order of Operations can be boiled down into three “real” operations.

Parenthesis are merely a way to group things – they aren’t a real operation. So they doesn’t count as a real operation.

Since division is really just multiplication turned upside down, we don’t need to include it separately, either. Likewise, subtraction is addition on its ear. So we throw him out, too.

Now we have only three: exponents, multiplication and addition.

Exponents are the shortcut for multiplication.

In a previous article about remembering exponent rules, I recorded this video about exponents:

You see that 3 x 3 x 3 x 3 is 3⁴. The exponent is the shortcut for multiplication.

Multiplication is the shortcut for addition.

Likewise, when we get overwhelmed with adding up the same numbers over and over, like in the video, 4 + 4 + 4 + 4 + 4, we can use multiplication to shortcut it: 5 x 4.

Follow the shortcut evolution.

The shortcut evolution is like this
1. Addition came first.
2. Then we created multiplication to make addition easier.
3. Then we created exponents to make multiplication easier.
So when you do arithmetic, we should do the “recent” shortcuts first (exponents) and then the “older” shortcuts (multiplication) and then the “regular” arithmetic (addition). Remember that subtraction is addition and division is multiplication.

And keep in mind that we need to watch the grouping or anything isolated with parenthesis, absolute value bars or in a fraction. The grouping/isolation tools always trump the other operation rules.

What if your answer isn’t the same as the back of the book?

Some textbooks actually have multiplication done before division. This means that the problem 9 ÷ 3 x 2 will show a different answer (3/2) in that textbook’s solution pages than what you would get following the OoO I’m describing here (6). These texts are rare, but I’ve seen them. So keep your eyes peeled.

The Order of Operations is a set of rules that we’ve agreed on. Which means that as long as a textbook clearly defines their order that they will follow, they can do things like this.

If you get confused as to which to do first, demand parenthesis. (Yes, you can do that.) Or put parenthesis into your child’s textbook to help them out.

The problem sets should be there to enforce, not confuse.

What do you think? Does this help or hinder the way you’ve always viewed the Order of Operations? Share your thoughts in the comments.

Related articles
July 4, 2011
How to Teach Math Concepts at the Dinner Table
Would you like to teach math everywhere you go? Well, here’s one from the table!

Daughter enjoys playing with our salt-and-pepper shaker holder at dinner. She takes out the salt, then takes out the pepper, then replaces the salt, then replaces the pepper.

The order in which she does these four operations vary. Including switching the salt and pepper.

She’s slowly putting together the pieces that will one day become the commutative property.

She’s also practicing substitution…

She’s learning that the salt and pepper can be switched (commutative). And she’s learning that one can be interchanged for the other (substitution).

…and the associative property!

She attempted to put her small milk cup into the holder. It fit, but only with pushing. She then removed the milk cup and attempted to put it in the other side. (At her age the things grown-ups understand are not obvious to her.)

Although non-equality isn’t part of the associative property (which is if a=b, b=c then a=c), the comparison of three things is.

Here are the things she’s learning from this dinner session:

This fact she discovers from interchanging them in the holder.

By putting them in the holder in a different order, she learns that the equality is commutative.

Since the milk cup won’t fit into the spot the salt was just in, she learns this.

And trying to shove the milk cup in the other side yields this fact.

So pull out the stops – give the children everything. And let them explore. If they have the gift of language, you can hint at some of these properties, but be careful not to go into a full “lesson” at dinner. Teaching math at the dinner table should be fun.

Where have you seen math properties in your world? Share your stories in the comments – or link back to your story on your blog!

Related articles
June 30, 2011
The Order of Operations Explained: Exponents
This is the 3rd in the series The Order of Operations Explained. For the other articles in this series, click here to visit the introduction.

Exponents are the second in the list for the Order of Operations (OoO).

When we want to find the result of 3² x (2 + 7), we have no problem. We know to do parenthesis and then exponents, then multiplication.

When you teach algebra, you’ll have to teach some distributing of exponents. But that’s still okay. And the rules of exponents are pretty straight up.

So why a whole article on exponents?

In the order of operations, the “Exponents” rule represents a bunch more than just superscripts or tiny numbers flying up and to the right of things.

Roots are exponents, too!

Tree Roots by Linda Allardice

Not the ones from trees, but things like square roots and cube roots. Consider $\sqrt9 + 2$ . You do the square root first because it qualified as an “exponent.”

But if you had $\sqrt{9+2}$ , the 9 + 2 is under the radical sign (the square root sign) so it’s bound together in the “Parenthesis” rule.

This one isn’t that hard with arithmetic, but when you come to algebra and start “undoing” these things – it’s important to remember that roots fall into this category.

Fractional exponents are exponents.

This one seems pretty “duh” so it’s easy to see how they fall into the “E” of the order of operations. But what are fractional exponents really?

$9^\frac{1}{2} \text{ means }\sqrt9$

So fractional exponents are the same as roots.

Note that some fractional exponents are roots and “plain” exponents all mixed up. Like this one:

$27^\frac{2}{3} \text{ means } \sqrt[3]{27^2} \text{ as well as } (\sqrt[3]{27})^2.$

This is a big fat full concept that needs a little more explaining. I’ll write more on these in another article.

Logs fall under the E.

Axe In Stump by caroline steinhauer

As my algebra and computer math teacher in high school, Mrs. Kelley, used to tell us – logarithms are exponents. It took me a long time to figure out what the heck she meant. But when I did, I thought it was brilliant.

This is a true statement: $\log_3 9 = 2$ . Let’s analyze it.

Based on the definition of logarithms, this means that 3² = 9. Which we know is true.

Notice who the exponent is in this: 3² = 9: 2 is the exponent. And 2 is the same as $\log_3 9$ because the equals sign in $\log_3 9 = 2$ means “is the same as.” So the logarithm $\log_3 9$ is the exponent 2.

Still with me? Either way, it’s okay. It’s a weird concept that I can go into detail in a video soon.

The thing to remember here is that logarithms fall into the “Exponents” rule of the order of operations.

So if you have $\log_3 9 + 7$ , you have to do the $\log_3 9$ first and then add the 7 after.

Want more on exponents?

In the meantime, you can check out more than everything you always wanted to know about exponents on the Wikipedia Exponents page. Rebecca Zook created a great video on logarithms. And check out this explanation and problems to work on fractional exponents.

And let me know what you think. Did I miss something?

Related articles
- How Calculators Inhibit Learning the Distributive Property in Algebra
- What’s the Domain, Why You Need It and How You Get It
June 26, 2011
The Order of Operations Explained: Parenthesis
This is the 2nd in the series The Order of Operations Explained. For the other articles in this series, click here to visit the introduction.

I mentioned in the introductory article for this series that “the order of operations isn’t best practice for expressions involving variables.”

When you involve a variable, you can’t just “do” the arithmetic. Like in the case of 2(3x + 4)=11. You can’t add 3x and 4 to get a result before moving on. You have to use the distributive property.

And even the distributive property won’t work sometimes – as in the case of absolute values shown below.

Parenthesis mean isolation.

When we say “parenthesis” in the Order of Operations (OoO for short), we mean anything that’s grouped together and isolated. This could mean with actual parenthesis. This could mean [square brackets] or {curly brackets}.

Although grownups seem to know that square and curly brackets are the equivalent of parenthesis, children don’t. This has to be said out loud.

“Parenthesis” in the OoO can also mean |absolute value bars|. This one’s not so clear.

When you try to solve the equation 4|2x+3|=20, you have to start with dividing by 4 to isolate the absolute value chunk. There’s not a “rule” for distributing the 4.

(Although, it would be worth it, and fun, to see if your children can come up with some rules for distributing within absolute value bars. This would be some real mathematics at work for them – experimenting and discovering.)

Tops and bottoms of fractions are implied parenthesis.

It’s also the case that the numerator (top) and denominator (bottom) of a fraction are isolated places. These fall under the OoO as parenthesis.

Check out this older video I did. It shows how this works with fractions:

Parenthesis are for deviation from the other rules.

David Chandler of Math without Borders commented this in the previous article of this series:

The rule is to do higher level operations first. Use parentheses whenever your intention is to deviate from this rule.

If you can focus on this instead of a mnemonic device, you can get students to internalize what’s going on with the OoO. It’s important, however, to make sure they remember about other bracket shapes as well as isolation.

Let us know your tips and thoughts on the P in PEMDAS!

Related articles
June 19, 2011