I was at a seminar yesterday with world famous (and awful fun) Thiagi. He keeps his participants on their toes with small activities called jolts. Jolts are defined at interactive experiential activities and:
…force participants to re-examine their assumptions and revise their habitual practices.
One jolt we did yesterday got me to thinking about math. Okay, many of them had me thinking about math. But this one was about the multiplication principal of counting and sets.
The multiplication principal says that if you have 7 ways to do the first thing and 3 ways to do the 2nd thing, then you’ll have 3 * 7 = 21 ways to do them together. Assuming you pick one of each.
So if I want a sandwich (tuna, ham or turkey) and a side (chips, onion rings, fruit or fries) for lunch, I will have the option of 3 * 4 = 12 different lunches.
The Thiagi Circles Jolt
Here is the Circles Jolt that Thiagi offered: Draw this figure without ever lifting your pencil or retracing over any lines (or curves):
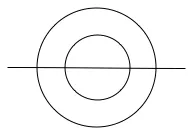
It isn’t hard, as you probably see. It takes anywhere from 10 to 45 seconds to figure it out. The question is, “Is there another way to do it than the one I thought of?”
So here are the ways I immediately thought of in the Thiagi Workshop:
The fancy pants teacher’s pet, Mark, was asked to demonstrate the answer. And he did it in an even different way! So I saw that there were 8 more ways to do it:
Trying to trump Mark and be the new teacher’s pet, I announced that there were indeed 16 ways to accomplish Thiagi’s goal.
And here I am. Still trying to win the favor of the teacher by producing the 16 ways via blog and video.
There are 16 ways because of the Multiplication Principal of Counting.
Notice there are four questions to answer when solving this:
- Do you start from left or right side of the drawing?
- Do you start by drawing the outer circle or go through and start at the inner circle?
- Do you go up or down on the first circle you draw?
- Do you go up or down on the second circle?
Each question has two different options. So there are
2 sides to start from * 2 circles * 2 directions to go in the 1st circle * 2 direction in the 2nd circle
2 * 2 * 2 * 2 = 16 different ways to draw the diagram!
Teach this with experiments.
Although you now know how many there are, don’t teach it this way. Instead, just give the jolt to the kids. Once they solve it, show them “your way,” which should be any way that is different than theirs.
Then tell them that for ever unique solution, you’ll give them $1. (Thiagi gave out $1 bills yesterday, too!)
Once they come up with all 16, offer the extra $4 for some way they can show the number 16 with numbers (logically based on their solutions). They might come up with 2 * 8 or 4 * 4, as long as they can group their drawings in logical bundles.
What do you think?





