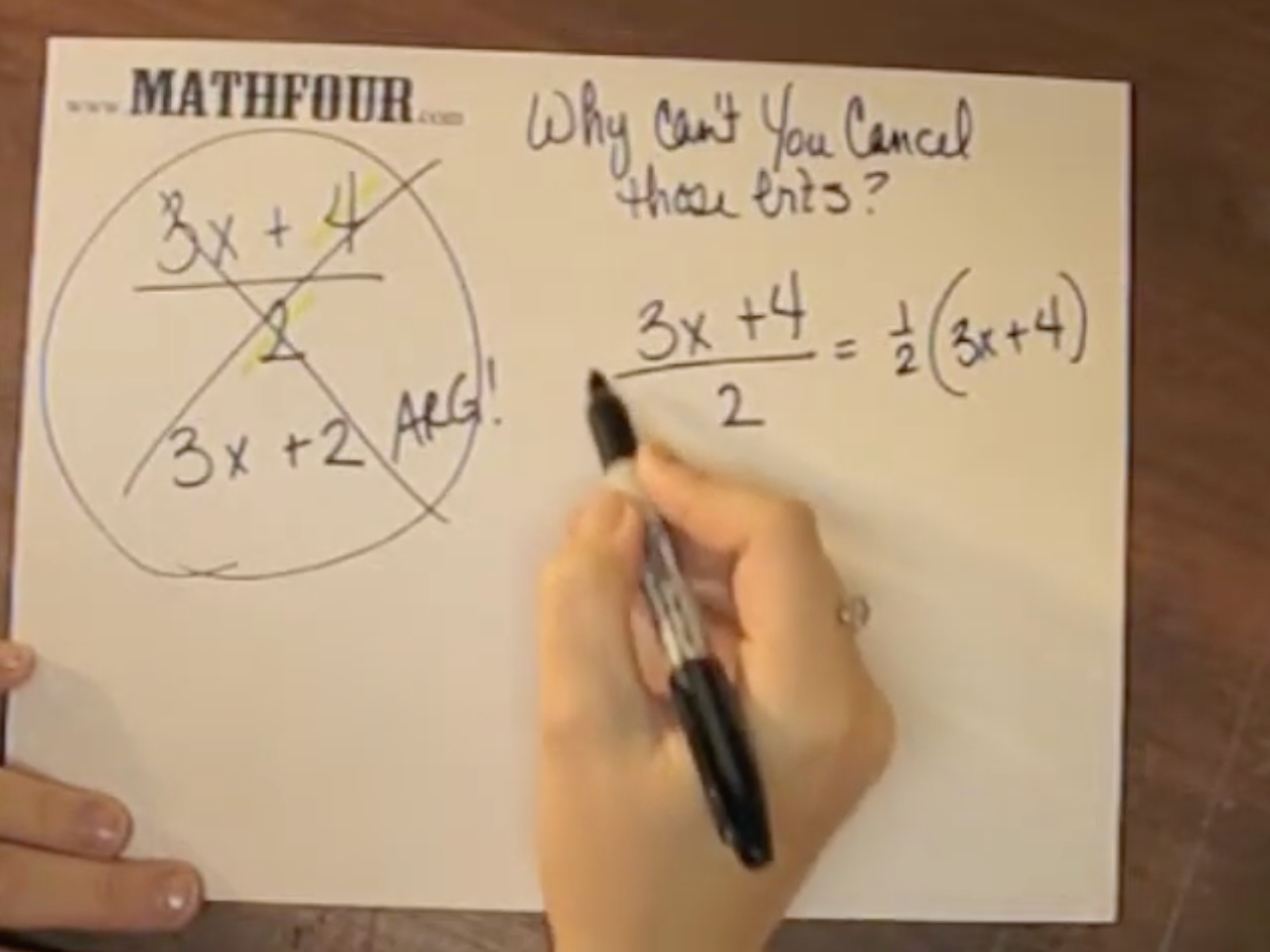distributive property

The Distributive Property — What Is It, Anyway?

The two most commonly used operations in math are addition and multiplication.

And although we intermingle addition with multiplication (along with division and subtraction), these two can only mix using the distributive property.

How the distributive property works

Multiplication, in a crude sense, is a shortcut of addition. Like 3 x 8 is the number 8 added to itself three times. Or 8 + 8 + 8.

Look at 3 x (6 + 2). This is the number (6 + 2) added to itself three times. (Refrain from adding those two together, no matter how tempting. Leave them separate as 6 + 2.)

So we have (6 + 2) + (6 + 2) + (6 + 2).

And we know that when it comes to only adding, we don’t need any parenthesis. Which gives us

6 + 2 + 6 + 2 + 6 + 2

Also, addition is commutative. So we can scramble these numbers around.

6 + 6 + 6 + 2 + 2 + 2

And if we want, we can squish them together in parenthesis (seems lame, but stay with me…)

(6 + 6 + 6) + (2 + 2 + 2)

And, hey! We know that 6 + 6 + 6 means 3 x 6 (and the same with 2’s) so we have:

(3 x 6) + (3 x 2)

Remember what we started with. Put it together with what we ended with. And we’ve just demonstrated (the long way) that

3 x (6 + 2) = (3 x 6) + (3 x 2)

or, more visually…

3 x (6 + 2) = (3 x 6) + (3 x 2)

This is the Distributive Property of Multiplication Over Addition. (That’s the fancy name for the distributive property.)

It works with something else, too…

Since exponents are a shortcut of multiplication, we can play the same game.

Consider (6 x 2)³

This is (6 x 2) x (6 x 2) x (6 x 2)

And we can get rid of parenthesis and scramble:

6 x 6 x 6 x 2 x 2 x 2

And re-group:

6³ x 2³

Showing that:

(6 x 2)³ = 6³ x 2³

This, by the way, is the Distributive Property of Exponentiation Over Multiplication!

Yes — this IS useful.

Seems ridiculous, right?

But when learning algebra, students often get lost when faced with 3(y + 2). “What do I do now?” they think, going into panic mode.

If they know that y is just a number with lipstick on (as a disguise), they can think about the above example.

Remembering what it means is the key to knowing what to do with the algebra stuff!

What do you think? Share your thoughts in the comments or on twitter/x.

You might also like:

November 6, 2012

How Calculators Inhibit Learning the Distributive Property in Algebra

Do you wonder if your children should be using a calculator “at their age”? Are you a fan of calculators, but have friends who aren’t? Are your friends “into” calculators while you oppose them?

I often hear people say that children 50 years ago understood math concepts more quickly. Although our parents weren’t taking classes called algebra in the 7th grade, they were doing algebra in the 7th grade.

Algebra is arithmetic.

There are two fundamental and rarely understood facts about algebra:

Algebra is arithmetic with one or more numbers in disguise.
Algebra has exactly the same rules as arithmetic.

Which means if you can do arithmetic you already know how to do algebra!

Our parents or grandparents, 50 or even 30 years ago, weren’t using calculators. They had to apply all the rules of arithmetic to get the job done. Which means that they had to apply all the rules of algebra.

Teaching them a class called “Algebra” was much easier because of this.

What are the rules?

The basic rules that non-calculator users must apply are the distributive property and the order of operations. The distributive property is the thing that calculator use eliminates.

Children could get practice mentally multiplying things like 3 x 86 and do 3(80+6) = 240+18=268. With this practice, they are ready for 4x(3y+2z) = 12xy+8xz.

If they never have to multiply 3 x 86 in their head, they never get the experience of the distributive property. Which means teaching them 4x(3y+2z) = 12xy+8xz will cause anxiety and frustration. They see it as “magic” or “something you made up just to confuse me.”

Give them the tools they need.

Refuse to let students have the calculator. Let them have the tool of the distributive property for algebra before you teach them “Algebra”. Give them the benefit our parents and grandparents had!

Those Pesky Exponents – How to Distribute Exponents over Multiplication

Remember that you can distribute multiplication over addition? You can also distribute exponents over multiplication.

Here’s how and why it works:

And here it is written out “long ways” for an algebra problem. Remember, you can use the short version. I do the videos with the long version to help you remember why it works.

Have any questions? Post them in the comments!

February 2, 2011

How to Multiply By Hand Without Hurting Your Brain

There’s an amazingly fancy tool that I began discussing in the last post. This D-word probably has been a close friend of yours for a while. It’s likely you’ve used it before and just didn’t realize it.

Well, now you can give it a name and give it some practice. It’s the Distributive Property.

Fancy name. Fabulous friend.

Check out what’s really going on with 87 x 48 here…

That one you can do quickly with pencil and paper. Here’s an easier one that you are more likely to do in your head (after practice with P&P of course)…

Have you done this before? Share your stories in the comments.

January 26, 2011

How and When to Cancel Things in Fractions

One of the common errors in algebra is canceling bits in fractions that can’t be canceled. To remember the rule, though, you don’t have to memorize anything. You only have to think of a plain arithmetic problem to compare it.

To help you remember what’s allowed with problem:

\frac{3x+4}{2}

think about this simpler problem:

\frac{8+4}{2}

Like this:

And just to keep you straight, here are the requirements (and a couple of examples) for the fancy <cue music> “distributive property.”

What do you think of this explanation? Post your thoughts in the comments.

January 25, 2011

Tag: distributive property