Tag: geometry

  • Fahrenheit to Celsius – Graphically!

    Fahrenheit to Celsius – Graphically!

    Part of Wordless Wednesday…

    The beautiful and talented Heather at Freebies4Mom.com sent me a post on An Easy Way to Convert Celsius to Fahrenheit.

    It inspired me to draw the graphs of Celsius in terms of Fahrenheit and Fahrenheit in terms of Celsius.

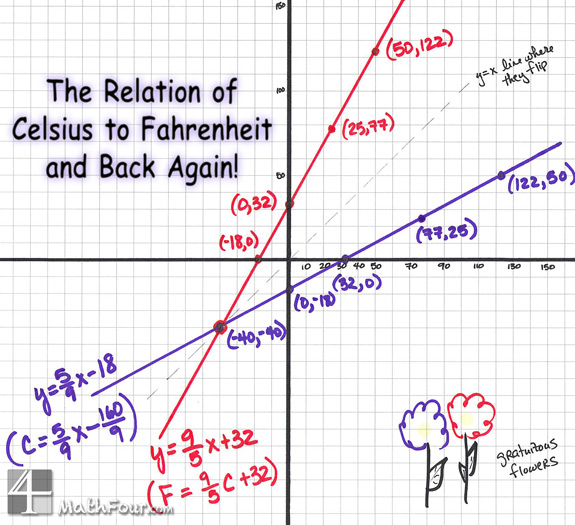
    The conversion from Celsius to Fahrenheit and back again can be strange. One way to understand it is on a graph. And you can use this to teach some linear algebra too!

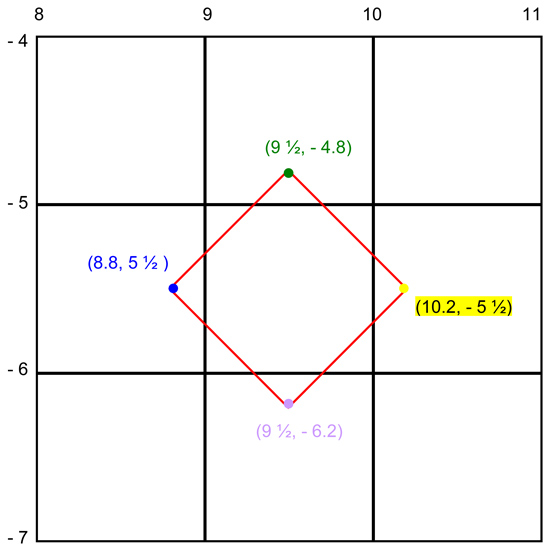
    Notice these two intersect at (-40, -40). Which means that -40°F is -40°C!

    Use it to convert temperatures.

    The x values on the red line are Celsius – so find the °C you have and then look at the y-value to convert to °F.

    It’s just the opposite on the purple line.

    Okay, fine. This isn’t the greatest way to convert – but it’s exciting to see it graphically. And it might be easier to convert this way for someone who’s more visual.

    Use it to teach math!

    These two lines are inverses of each other. So the coordinates of one are switched to make the other.

    Also, they mirror image across that 45° line. I marked the line with dashes and wrote $latex y=x$ on it.

    And if you’re into this, their functional composition (both ways) is… x! (not factorial)

    Compare and Contrast…

    Take a look at the way J.D.Roth did it and then look at the graphs I have. Let your students find the way they like the best. And encourage them to create new ways!

    Oh, yeah – and share what happens in the comments!

  • Teaching Geometry with Pickles

    Teaching Geometry with Pickles

    Daughter is into pickles. Like way into pickles. If I were to start a blog just for her, it would be called www.PicklesAndPretzels.com. (She’s also into pretzels.)

    So when Husband grabbed two instead of one jar yesterday, it seemed natural.

    Unloading the groceries, I saw the two jars a little more closely.

    “Holy cow,” thought I. They’ve made ellipses (pickle ovals) out of segmenting cylinders (the whole pickles)! And they’re marketing them!

    Math in action – via Vlasic!

    Interested in more about ellipses? Check out Wolfram MathWorld’s bit on it.

    Related articles
  • Cuisenaire Rods Go Pythagorean!

    Cuisenaire Rods Go Pythagorean!

    I’ve been playing with the lovely Cuisenaire Rods for a few weeks now. I made the (fortunate) mistake of creating this flower in a past article about coordinate pairs.

    The mistake was that I would eventually have to come up with the coordinates for this thing. Fortunate because it gives the MathFourTicians out there something else to teach with the rods!

    The center of the flower is the place to start.

    Since all the “petals” are attached to the center, that’s probably the best place to begin.

    I converted to something I could see.

    Since everything is tiny (1 cm), I went to a bigger setup. And some of the coordinates were easy to pick out. So I put those in the big grid, too:

    And then I started to do some work…

    Next I considered what I was really dealing with: a square. And each side was 1 cm.

    According to those crazy Pythagoreans, the diagonal measures 2\sqrt2:

    So half the diagonal is 22\frac{\sqrt{2}}{2}:

    I went back to the big grid.

    When I put this information on the big grid, it looks like this:

    Doing some arithmetic and geometry, I get:

    Using my very cool TI-30 calculator, I get that 22−12≃0.2\frac{\sqrt{2}}{2}-\frac{1}{2}\simeq0.2.

    I can accurately name the points!

    Knowing that each corner pokes out roughly 0.2, I can calculate the coordinates:

    From this I can create the ordered quadruples as described here for the petals of the flower. But at this point I’m pretty much needing a break. So I’ll leave that for next time.

    Whatcha think? Fun? Share your thoughts in the comments and on Twitter:

    Related articles