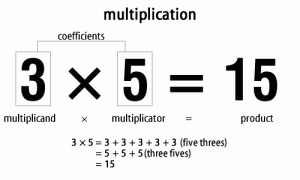
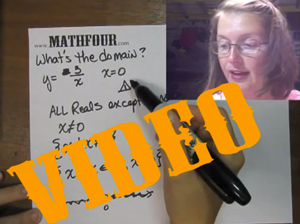When we teach math at home, we start with the counting numbers. Then we move to either the homeschool or classroom setting and build on those with negatives. And zero is sometimes left behind.
Zero seems to be an understood concept because it’s so much a part of our lives, as grownups. But zero is a very unusual bug.
Is Zero Positive?
We think of the numbers as either positive or negative.
But actually, all real numbers can be divided into three categories: positive, negative and zero.
This is one of the reasons zero can be forgotten in all this mix. With so many other numbers to be positive and negative, zero’s truly in a class by himself.
Notice I wrote “All real numbers can be divided into three categories.” Imaginary and complex numbers can’t be classified this way. You can order imaginary and complex numbers, but you have to do it without labeling them as positive or negative.
Why can’t we just say zero is positive?
I guess we could. But you might not want to when you see this…
In math, sometimes, we do things because if we didn’t, they’d mess everything else up.
This is one of those situations.
So let’s say 0 is positive, just for the minute.
Take the rule, “When multiplying, if the signs are different, the result is negative.” So then (positive) zero times negative 3 is (negative) zero. Like this:
0 x -3 = +0 x -3 = -0
But we determined that zero was positive!
So this messes things up. Therefore, zero needs to be in a class by himself.
But zero feels positive and negative, sometimes!
Indeed if a kid doesn’t owe his sister anything, that’s a positive feeling.
If you owe someone $3, then you can say you have negative 3 dollars. So if you owe them nothing, don’t you have a negative zero dollars?
This is more of a direction than a positive or negative sign. The “vector” (arrow in a direction) that has length zero can technically be pointing in any direction. It doesn’t matter. And that’s what’s going on when you think of zero as positive or negative. You think of owing (money going in a direction) nothing.
But remember, that’s only thinking of zero as positive or negative. He really isn’t either.
He’s just zero.
Check out the classic Schoolhouse Rock Multiplication Rock video and let me know what you think of all this zero talk.