Kathy at Nova Beads helped me “tie them off” and choose the hangers. The end result is beautiful!

Have questions about probability or making jewelry with it? Ask in the comments!


Kathy at Nova Beads helped me “tie them off” and choose the hangers. The end result is beautiful!

Have questions about probability or making jewelry with it? Ask in the comments!


I was at a seminar yesterday with world famous (and awful fun) Thiagi. He keeps his participants on their toes with small activities called jolts. Jolts are defined at interactive experiential activities and:
…force participants to re-examine their assumptions and revise their habitual practices.
One jolt we did yesterday got me to thinking about math. Okay, many of them had me thinking about math. But this one was about the multiplication principal of counting and sets.
The multiplication principal says that if you have 7 ways to do the first thing and 3 ways to do the 2nd thing, then you’ll have 3 * 7 = 21 ways to do them together. Assuming you pick one of each.
So if I want a sandwich (tuna, ham or turkey) and a side (chips, onion rings, fruit or fries) for lunch, I will have the option of 3 * 4 = 12 different lunches.
Here is the Circles Jolt that Thiagi offered: Draw this figure without ever lifting your pencil or retracing over any lines (or curves):
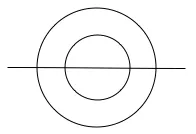
It isn’t hard, as you probably see. It takes anywhere from 10 to 45 seconds to figure it out. The question is, “Is there another way to do it than the one I thought of?”
So here are the ways I immediately thought of in the Thiagi Workshop:
The fancy pants teacher’s pet, Mark, was asked to demonstrate the answer. And he did it in an even different way! So I saw that there were 8 more ways to do it:
Trying to trump Mark and be the new teacher’s pet, I announced that there were indeed 16 ways to accomplish Thiagi’s goal.
And here I am. Still trying to win the favor of the teacher by producing the 16 ways via blog and video.
Notice there are four questions to answer when solving this:
Each question has two different options. So there are
2 sides to start from * 2 circles * 2 directions to go in the 1st circle * 2 direction in the 2nd circle
2 * 2 * 2 * 2 = 16 different ways to draw the diagram!
Although you now know how many there are, don’t teach it this way. Instead, just give the jolt to the kids. Once they solve it, show them “your way,” which should be any way that is different than theirs.
Then tell them that for ever unique solution, you’ll give them $1. (Thiagi gave out $1 bills yesterday, too!)
Once they come up with all 16, offer the extra $4 for some way they can show the number 16 with numbers (logically based on their solutions). They might come up with 2 * 8 or 4 * 4, as long as they can group their drawings in logical bundles.
What do you think?


Yesterday’s post showed how to tell the difference between permutations and combinations. The day before, I posted about n! and what the heck to do with it. Now you’re ready to do some calculations.
Here’re the two formulas and how they compare:
And here are the numbers worked out from the video above:
Here’s an application of it using the cat example from the first video of yesterday’s post:
Post your questions and thoughts in the comments section.


Have you ever taught permutations and combinations?
Do you use the words, “In permutations, order matters”?
There are lots of permutation problems where there’s no ordering whatsoever. But they are still permutations. So telling the difference between a combination and permutation can be difficult if you use the ol’ “order matters” rule. Like this:
Notice there was no “order” in the permutation – each cat is having something different done with it. (And woe for the cat who’s being eaten.)
The real differentiating factor between permutations and combinations is this:
If the things being chosen are going to do (or have done to them) the same thing, it’s a combination.
and
If the things being chosen will do (or have done to them) different things, it’s permutation.
Here’s another example, along with a tip to choosing which to use:
Will this help your students? And check out the next post on how to do the calculations for these.


My favorite professor in college used to pronounce n! as “n, dammit.” He was awesome, and a true rogue!
The “proper” way to pronounce it is “n factorial.” And here’s what it means:
When working with factorials, it is important to remember what can and can’t be done. Here’s how to use them in fractions:
You will have to work with factorials in Permutations and Combinations (info on those coming tomorrow). Here’s what factorial work will look like then:
These are all important steps for the upcoming post on Wednesday about “How to Calculate Permutations and Combinations”.
Questions? Need the info faster? Post your thoughts and questions in the comments section.
